
Paralelkenar Formülleri Nelerdir?
Paralelkenar, geometri alanında önemli bir dörtkendir ve çeşitli formülleri ile çeşitli uygulamalarda yer alır. Bu yazıda, paralelkenarın tanımı, alan ve çevre hesaplama yöntemleri ile köşegen uzunlukları gibi temel özellikleri ele alınmaktadır.
Paralelkenar, matematikte ve geometri alanında önemli bir şekil olarak tanımlanır. İki çift paralel kenardan oluşan bu dörtgen, çeşitli özellikleri ve formülleri ile dikkat çeker. Bu makalede, paralelkenar ile ilgili temel formüller, özellikler ve uygulama alanları detaylı bir şekilde ele alınacaktır. Paralelkenarın Tanımı ve Özellikleri Paralelkenar, iki çift paralel kenarın oluşturduğu bir dörtgendir. Aşağıdaki özellikleri ile tanınır:
Paralelkenarın Alanı Paralelkenarın alanı, taban uzunluğu ve yüksekliği kullanılarak hesaplanır. Alan formülü şu şekildedir: A = a h Burada:
Yükseklik, tabana dik olarak çizilen bir doğrudur. Paralelkenarın alanını hesaplamak için, taban uzunluğu ve yükseklik değerleri bilindiğinde bu formül kullanılabilir. Paralelkenarın Çevresi Paralelkenarın çevresi, kenar uzunluklarının toplamı ile hesaplanır. Çevre formülü şu şekildedir: C = 2(a + b) Burada:
Bu formül ile paralelkenarın her iki kenarının toplamının iki katı alınarak çevre hesaplanır. Köşegenler Paralelkenarın köşegenleri, şeklin köşelerinden çizilen doğrular olup, birbirini ortalar. Köşegenlerin uzunluğu, aşağıdaki formülle hesaplanabilir: d1 = √(a² + h²) d2 = √(b² + h²) Burada:
Bu formüller, paralelkenarın köşegenlerinin uzunluğunu belirlemek için kullanılabilir. Uygulama Alanları Paralelkenar, mühendislik, mimarlık ve çeşitli bilim alanlarında yaygın olarak kullanılan bir şekildir. Alan hesaplamaları, malzeme tasarımı ve yapısal analizlerde paralelkenar formülleri önemli bir rol oynamaktadır. Ayrıca, matematiksel modelleme ve geometri derslerinde de sıkça karşılaşılan bir konudur. Sonuç Paralelkenar, geometrik yapısı ve hesaplama yöntemleri ile önemli bir şekildir. Alan, çevre ve köşegen uzunlukları gibi temel formüller, bu şeklin analizinde ve uygulamalarında büyük öneme sahiptir. Geometri derslerinde öğrenilen bu formüller, çeşitli bilimsel ve mühendislik alanlarında pratikte kullanılabilmektedir. Bu makale, paralelkenar ile ilgili temel bilgileri ve formülleri sunarak konunun daha iyi anlaşılmasına katkı sağlamayı amaçlamaktadır. |
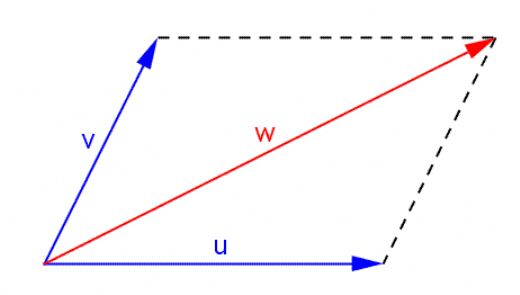















































Paralelkenar ile ilgili öğrendiğim en ilginç şey, iç açıların toplamının 360 derece olması. Özellikle komşu açıların toplamının 180 derece olduğunu düşündüğümüzde, paralelkenarın simetrik yapısı çok dikkat çekici. Paralelkenar iç açı toplamı, geometri derslerinde sıkça karşılaştığımız bir konu.
İlginç Gözlemler
Olgaç, paralelkenarların iç açıları hakkında yaptığın gözlemler gerçekten dikkat çekici. Paralelkenarın simetrik yapısı, geometri derslerinde sıkça karşımıza çıkan bir konu olmasının yanı sıra, birçok farklı geometrik şeklin de temelini oluşturan bir kavram.
İç Açıların Toplamı
Paralelkenarın iç açıları toplamının 360 derece olması, birçok kişi için ilginç bir noktadır. Bu özellik, geometrinin temel kurallarından biridir ve farklı şekillerin de bu kurallar çerçevesinde nasıl oluşturulduğunu anlamamıza yardımcı olur. Özellikle komşu açıların toplamının 180 derece olduğunu bilmek, paralelkenarın simetrik özelliklerini daha iyi anlamamıza olanak tanır.
Geometri Dersleri
Geometri derslerinde bu tür konularla sıkça karşılaşmak, matematiksel düşünme becerimizi geliştirir. Paralelkenar gibi şekillerin özelliklerini öğrenmek, daha karmaşık geometrik kavramları anlamamızda önemli bir adım. Bu yüzden, paralelkenar gibi temel şekiller üzerine düşünmek ve soru sormak oldukça faydalı.
Paylaştığın düşünceler için teşekkürler! Geometriye olan ilginin artarak devam etmesi dileğiyle.
Paralelkenar nedir? Geometri derslerinde sıkça karşılaştığımız bu şekil, iki çift paralel kenardan oluşan bir dörtgendir. Karşı kenarlar eşit uzunluktadır ve çeşitli özellikleri ile dikkat çeker. Ayrıca alan ve çevre hesaplamalarında önemli bir yere sahiptir.
Paralelkenar Nedir?
Gökünur, paralelkenar, geometri derslerinde sıkça karşılaştığımız önemli bir şekildir. İki çift paralel kenardan oluşan bir dörtgen olmasıyla birlikte, karşı kenarların eşit uzunlukta olması, paralelkenarın temel özelliklerinden biridir. Bu şekil, alan ve çevre hesaplamalarında da büyük bir öneme sahiptir.
Alan Hesabı
Paralelkenarın alanı, taban uzunluğuyla yüksekliğin çarpılmasıyla bulunur. Yani, A = taban x yükseklik formülü kullanılarak hesaplanır. Bu özellik, pratikte birçok problemde karşımıza çıkar.
Çevre Hesabı
Çevresi ise, tüm kenarların toplamı olarak hesaplanır. Yani, C = 2 x (a + b) formülüyle ifade edilir; burada 'a' ve 'b' paralelkenarın iki farklı kenar uzunluğudur.
Bu temel bilgiler, paralelkenarın geometri derslerindeki önemini ve kullanım alanlarını daha iyi anlamamıza yardımcı olur.
Paralelkenarın özellikleri hakkında bilgi sahibi olmak, geometri derslerinde oldukça önemlidir. Özellikle paralelkenarların kenarları ve açıları arasındaki ilişkiler, alan hesaplamalarında da kritik rol oynar. Paralelkenarın köşegenlerinin özellikleri de dikkat çekicidir. Paralelkenarın özellikleriyle ilgili bir soru sorabilir misin?
Merhaba Remiz,
Paralelkenarın Kenarları ve Açıları
Paralelkenarların kenarları arasında eşitlik ve paralellik ilişkisi bulunur. Aynı zamanda, karşılıklı açıların eşit olduğu bilinmektedir. Örneğin, iki karşıt kenar eşit uzunluktadır ve iki karşıt açı da eşittir.
Paralelkenarın Köşegenleri
Paralelkenarın köşegenleri ise birbirini ortalar. Yani, bir paralelkenarın köşegenleri kesiştiğinde, her biri diğerini iki eşit parçaya böler. Bu özellik, alan hesaplamalarında ve geometrik kanıtlamalarda oldukça faydalıdır.
Soru Önerisi
Paralelkenarın alanını bulmak için, bir kenar uzunluğunu ve ona karşılık gelen yüksekliği kullanarak hesaplama yapılır. Eğer bir paralelkenarın taban uzunluğu 8 cm ve yüksekliği 5 cm ise, bu paralelkenarın alanını nasıl hesaplayabilirsiniz?
Bu sorunun cevabını bulmak, paralelkenarların özelliklerini anlamanızı pekiştirecektir. İyi çalışmalar dilerim!
Paralelkenar nedir? Benim için bu sorunun cevabı, karşılıklı kenarların paralel ve eşit olduğu dörtgenlerin varlığıyla başlar. Bu tanım, geometri derslerinde sıkça karşılaştığımız bir kavram. Özellikle paralelkenarların özellikleri arasında, karşılıklı kenarların uzunluklarının eşit olması ve açılarının belirli ilişkiler içinde olması dikkat çekiyor. Paralelkenarın alan formülü ile ilgili durum da oldukça ilginç. Alanın, herhangi bir kenarın uzunluğu ile o kenara ait yükseklik çarpımına eşit olduğunu öğrenmek, bu şeklin hesaplaması açısından oldukça pratik bir bilgi. Ayrıca, kenar uzunlukları ve açı derecelerinin bilinmesi durumunda alanın hesaplanması için kullanılan formüller de oldukça faydalı. Köşegenlerin özellikleri ise bir başka merak konusu. Köşegenlerin birbirlerini ortalaması ve alanı dörde eşit bölmesi, paralelkenarın simetrik özelliklerini daha iyi anlamamı sağladı. Geometri derslerinde bu tür detayları kavramak, şekillerin daha derinlemesine anlaşılmasına katkı sağlıyor. Sizce bu özellikleri bilmek, paralelkenarlarla ilgili problemleri çözme yeteneğimizi nasıl etkiliyor?
Paralelkenar Nedir?
Şevket, paralelkenar, gerçekten de geometri derslerinde sıkça karşılaştığımız önemli bir dörtgen türüdür. Karşılıklı kenarlarının hem paralel hem de eşit olması, bu şekli diğer dörtgenlerden ayıran temel özelliklerden biridir. Bu özellik, paralelkenarların simetrik yapısını ve alan hesaplamalarındaki kolaylığı sağlar.
Alan Hesaplama
Alanı hesaplamak için, herhangi bir kenarın uzunluğuyla o kenara ait yüksekliğin çarpımı yeterlidir. Bu basit formül, alan hesaplamalarını son derece pratik hale getirir. Aynı zamanda kenar uzunlukları ve açıların bilinmesi durumunda farklı formüller kullanarak alanı bulmak, geometri derslerinde önemli bir beceri kazandırır.
Köşegenlerin Özellikleri
Köşegenlerin birbirini ortalaması ve alanı dörde eşit bölmesi, paralelkenarın simetrik özelliklerini pekiştirir. Bu gibi detayların anlaşılması, geometri derslerinde şekillerin daha derinlemesine kavranmasını sağlar.
Sonuç olarak, bu özellikleri bilmek, paralelkenarlarla ilgili problemleri çözme yeteneğimizi büyük ölçüde etkilemektedir. Özellikle karşılıklı kenarların eşitliği ve köşegenlerin özellikleri, bu tür problemleri daha hızlı ve doğru bir şekilde çözmemize yardımcı olur. Geometri bilgimizi pekiştirmek için bu tür kavramları detaylı bir şekilde incelemek oldukça faydalıdır.