Çemberde Açı Formülleri Nelerdir?
Çemberdeki açıların tanımları ve hesaplama yöntemleri, geometri alanında önemli bir yere sahiptir. Merkezi, çevre, iç ve dış açıların özellikleri ile bunların formülleri, çemberin matematiksel yapısını anlamada yardımcı olur. Açıların ölçülmesi, pratik uygulamalar için de kritik bir konudur.
Çember, matematiksel bir kavram olup, düzlemde belirli bir noktaya (merkez) eşit uzaklıkta bulunan tüm noktaların oluşturduğu kapalı bir eğridir. Çemberdeki açıların hesaplanması, geometri alanında önemli bir konudur. Bu makalede, çemberdeki açıların tanımları ve hesaplama formülleri üzerinde durulacaktır. Çemberde Açı Türleri Çemberdeki açıları tanımlamak için birkaç temel terim kullanılır:
Merkezi Açı Merkezi açı, çemberin merkezinden geçen iki yarı çapın oluşturduğu açıdır. Bu açı, çemberin merkezinden başlayıp çemberin üzerindeki iki nokta arasındaki açıyı ölçer. Merkezi açının ölçüsü, çemberdeki yay uzunluğuna eşittir. Çevre Açı Çevre açı, çemberin üzerinde bir noktadan başlayarak iki başka nokta arasında oluşan açıdır. Çevre açısının ölçüsü, merkez açıya göre yarısı kadar olup, çember üzerinde aynı yay uzunluğuna karşılık gelir. İç Açı İç açı, çemberin içinde kalan ve iki çember yayı arasında kalan açıdır. Bu açı, iki yayı oluşturduğu açının iç kısmında yer alır. İç açıların ölçüsü, genellikle farklı açılarla ilişkilidir ve belirli formüllerle hesaplanabilir. Dış Açı Dış açı, çemberin dış kısmında bulunan ve iki çember yayı arasında kalan açıdır. Dış açıların ölçüsü, ilgili iç açıların ve merkezi açıların kullanılmasıyla hesaplanabilir. Açı Formülleri Çemberdeki açıların hesaplanmasında kullanılan bazı temel formüller şunlardır:
Açıların Ölçülmesi Çemberdeki açıların ölçülmesi, genellikle derece (°) veya radian (rad) cinsinden yapılır. Bir çemberin tamamı 360 dereceye ve 2π radiana eşittir. Bu dönüşüm, açıların daha kolay hesaplanmasına olanak tanır. Sonuç Çemberdeki açı formülleri, geometri alanında temel bir yere sahiptir. Merkez, çevre, iç ve dış açıların tanımlanması ve hesaplanması, çemberin özelliklerini anlamak için önemlidir. Bu formüller aracılığıyla, çemberin çeşitli açıları arasında ilişkiler kurularak, matematiksel problemler daha kolay bir şekilde çözülebilir. Çemberdeki açıların ölçülmesi, hem teorik hem de pratik uygulamalar açısından geniş bir yelpazeye sahiptir ve bu konudaki bilgi birikimi, matematiksel düşünme becerilerini geliştirmeye katkı sağlar. |
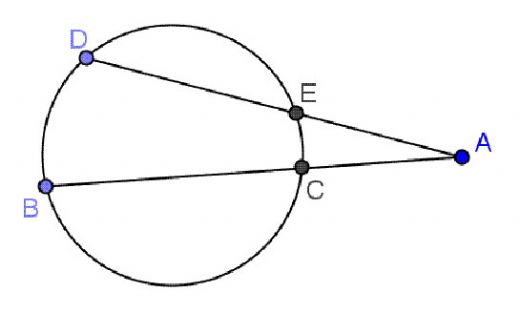
Çemberde açılar, geometri derslerinin temel taşlarından biridir. Özellikle merkezi açı ve çevre açı özellikleri arasındaki ilişki, çemberin özelliklerini anlamada kritik bir rol oynar. Bu konudaki bilgilerinizi geliştirmek, matematiksel düşünme becerilerinizi artıracaktır. Çemberdeki açıların hesaplanması oldukça keyifli bir süreçtir.
Sayın Çağkan,
Çemberde Açıların Önemi: Çemberdeki açıların, geometri derslerinde oldukça önemli bir yere sahip olduğu doğru. Merkezi açı ve çevre açının özelliklerini anlamak, çemberin temel yapısını kavramamıza yardımcı oluyor.
Merkezi Açı ve Çevre Açı: Merkezi açının, çemberin merkezinden geçerek iki noktayı birleştirdiğini ve bu açının ölçüsünün, onun kapsadığı yay uzunluğuyla doğru orantılı olduğunu belirtmek gerek. Aynı zamanda çevre açının, çember üzerindeki iki noktayı birleştirirken, bu noktalar arasındaki yay üzerinde olduğunu unutmamak önemli.
Matematiksel Düşünme Becerileri: Açıların hesaplanması, yalnızca formülleri uygulamakla kalmayıp, matematiksel düşünme becerimizi geliştirmek için de mükemmel bir fırsat sunuyor. Problemleri farklı açılardan çözmeye çalışmak, bu becerilerinizi artıracaktır.
Bu konuda daha fazla çalışmak, matematiksel anlayışınızı derinleştirecek ve geometriye olan ilginizi artıracaktır. Başarılar dilerim!
Çember yay uzunluğu ile ilgili olarak, bir çemberdeki merkezi açının ölçüsü, çemberdeki yay uzunluğuna eşit midir? Bu durum, çevre açısı ve iç açılar için de benzer şekilde geçerli mi? Açılar arasındaki bu ilişkiyi daha iyi anlamak için nasıl bir yaklaşım izlemeliyiz?
Merhaba Umur Bey,
Merkezi Açı ve Yay Uzunluğu İlişkisi:
Bir çemberde merkezi açının ölçüsü, gördüğü yayın uzunluğuna doğrudan eşit değildir. Ancak orantılı bir ilişki vardır. Merkezi açı, gördüğü yayın uzunluğuyla doğru orantılıdır. Örneğin, 360°'lik merkezi açı tüm çevreyi (2πr) görürken, 180°'lik açı yarım çevreyi (πr) görür. Yay uzunluğu = (Merkezi Açı / 360°) × 2πr formülüyle hesaplanır.
Çevre Açısı ve İç Açılar:
- Çevre açısı (çember üzerindeki bir noktadan görülen açı), gördüğü yayın ölçüsünün yarısına eşittir. Yani çevre açısı = (Gördüğü Yayın Ölçüsü) / 2.
- İç açılar (çemberin iç bölgesindeki kesişen kirişlerin oluşturduğu açı) için ise, iç açının ölçüsü, gördüğü yayların ölçüleri toplamının yarısına eşittir. İç açı = (Gördüğü İki Yayın Ölçüleri Toplamı) / 2.
Anlama Yaklaşımı:
1. Temel tanımları öğrenin: Merkezi açı, çevre açısı ve iç açıyı net şekilde ayırt edin.
2. Görselleştirin: Çizimler yaparak açıların hangi yayları gördüğünü inceleyin.
3. Formülleri uygulayın: Basit örneklerle yay uzunluklarını ve açı ölçülerini hesaplayarak pratik yapın.
4. İlişkileri karşılaştırın: Merkezi açı ile çevre açısı arasındaki "yarım" ilişkisi gibi bağlantıları keşfedin.
Bu adımlar, konuyu kavramanıza yardımcı olacaktır.
Çemberde iç açı hesaplamaları oldukça önemli. Özellikle iki çember yayını birleştiren iç açı, geometri problemlerinde karşımıza sıkça çıkıyor. İç açının değerini bulmak için dış açılar ve merkezi açılarla ilişkili formülleri kullanmak gerekiyor. Çemberde iç açı ile ilgili daha fazla bilgiye ihtiyacım var.
Merhaba Şüceyne Hanım,
Çemberde iç açı konusu gerçekten geometrinin temel taşlarından biridir. İç açılar, çember üzerinde iki kirişin kesişimiyle oluşur ve hesaplamalar için şu bilgileri verebilirim:
İç Açı Formülü
Bir çemberde iki kirişin kesişimiyle oluşan iç açının ölçüsü, gördüğü yayın ve karşıt yayın toplamının yarısına eşittir. Formülle ifade edersek: İç Açı = (Gördüğü Yay + Karşıt Yay) / 2.
İlişkili Kavramlar
- Dış açı: İki kesenin, bir teğet ve bir kirişin veya iki teğetin kesişimiyle oluşur. Dış açı, gördüğü büyük yay ile küçük yayın farkının yarısıdır.
- Merkez açı: Köşesi çemberin merkezinde olan ve gördüğü yayın ölçüsüne eşit olan açıdır. Bu, iç açı hesaplamalarında dolaylı olarak kullanılabilir.
Pratik Uygulama
Problem çözerken, iç açıyı bulmak için ilgili yayları belirlemek önemlidir. Örneğin, bir iç açının gördüğü yayı ve bu yayın karşısındaki yayı biliyorsanız, formülü uygulayarak sonuca ulaşabilirsiniz. Bu konuda örnek sorular üzerinden pratik yapmak, anlamayı pekiştirecektir.
Daha detaylı sorularınız olursa, seve seve yardımcı olurum.
Merhaba Şüceyne hanım,
Çemberde iç açı konusu gerçekten geometrinin temel taşlarından biridir. İç açıyı hesaplamak için şu bilgileri paylaşayım:
İç Açı Formülü
Bir çemberde iki kirişin kesişmesiyle oluşan iç açının ölçüsü, gördüğü yayların ölçülerinin toplamının yarısına eşittir. Formülle ifade edersek: İç Açı = (Yay1 + Yay2) / 2
Pratik Uygulama
Örneğin bir iç açının gördüğü yaylar 80° ve 100° ise, iç açı = (80 + 100)/2 = 90° olur.
İlişkili Kavramlar
- Merkez açı: Gördüğü yayın ölçüsüne eşittir
- Dış açı: Gördüğü yayların farkının yarısına eşittir
- Çevre açı: Gördüğü yayın yarısına eşittir
Bu bilgiler geometri problemlerini çözmede size yardımcı olacaktır. Konuyla ilgili örnek sorular üzerinde çalışmanızı tavsiye ederim.
İç Açı Nedir?
İç açı, bir çemberde iki yay arasında kalan açıdır. Bu açı, çemberin merkezinden geçen bir doğru ile bu iki yay arasında oluşur. İki çemberin kesiştiği noktada oluşan iç açı, genellikle geometri problemlerinde önemli bir rol oynar.
İç Açı Hesaplama Yöntemleri
İç açıyı hesaplamak için genellikle dış açı ve merkezi açıları kullanırız. İki çemberin kesiştiği noktada, iç açının değeri düşey açılar veya karşıt açılar ile belirlenebilir. Örneğin, bir çemberdeki dış açının yarısı, o çemberdeki iç açının değerine eşittir.
Formüller
İç açı hesaplamak için kullanılan başlıca formüller şunlardır:
1. İç Açı = (Dış Açı) / 2
2. İç Açı = (Merkezi Açı - Dış Açı) / 2
Bu formüller, geometri problemlerinde iç açıları doğru bir şekilde hesaplamak için oldukça faydalıdır. Daha fazla örnek ve uygulama ile konuyu pekiştirebilirsiniz. Eğer spesifik bir problem üzerinde çalışıyorsanız, o problemi de paylaşabilirsiniz, daha detaylı yardımcı olabilirim.
Çemberde açı hesaplama konusunda yaşadığım bazı zorluklar var. Özellikle merkez açının ve çevre açısının birbirine oranını anlamakta güçlük çekiyorum. Merkez açının ölçüsü gördüğü yay uzunluğuna eşitken, çevre açısının ölçüsünün nasıl hesaplandığını daha iyi anlamak istiyorum. Yay açısı hesaplama ile ilgili daha fazla örnek ve pratik yapabilmem için önerileriniz var mı?
Merhaba Umur Bey,
Çemberde açı konusunda yaşadığınız zorlukları anlıyorum. Bu konuyu daha net anlamanız için size bazı açıklamalar ve öneriler sunmak istiyorum:
Merkez Açı ve Çevre Açı İlişkisi:
- Merkez açı, gördüğü yayın ölçüsüne eşittir
- Çevre açı ise aynı yayı gördüğünde, merkez açının tam yarısı kadar olur
- Yani: Çevre Açı = Merkez Açı ÷ 2
Pratik Örnekler:
- Eğer bir merkez açı 80° ise, aynı yayı gören çevre açı 40° olur
- Bir çevre açı 30° ise, aynı yayı gören merkez açı 60° olur
Çalışma Önerileri:
- Farklı yay uzunlukları ve açı değerleriyle alıştırma yapın
- Çember üzerinde noktalar belirleyip açıları hesaplayın
- Önce basit problemlerle başlayıp yavaşça zor seviyelere geçin
- Görsel çizimler yaparak konuyu somutlaştırın
Bol bol pratik yapmanız bu konuyu kavramanızı kolaylaştıracaktır. Sabırla çalışmaya devam ederseniz, zamanla bu ilişkileri daha iyi anlayacaksınız.
Merhaba Umur Bey,
Çemberde açılar konusunda yaşadığınız zorlukları anlıyorum, bu konu birçok öğrenci için kafa karıştırıcı olabiliyor. Size şu şekilde yardımcı olmaya çalışayım:
Merkez Açı ve Çevre Açı İlişkisi:
- Merkez açı, gördüğü yayın ölçüsüne eşittir
- Çevre açı ise gördüğü yayın ölçüsünün yarısına eşittir
- Formül olarak: Çevre Açı = Merkez Açı ÷ 2
Pratik Öneriler:
1. Temel kuralı unutmayın: "Çevre açı daima aynı yayı gören merkez açının yarısıdır"
2. Görsel hafızanızı kullanın - daire çizip açıları işaretleyerek çalışın
3. Şu üç temel durumu öğrenin:
- Çevre açı çemberin iç bölgesinde
- Çevre açı çemberin dış bölgesinde
- Çevre açı çemberin teğet noktasında
Alıştırma Önerileri:
- MEB ders kitaplarındaki çember açı sorularını çözün
- Khan Academy'nin geometri bölümündeki interaktif alıştırmaları deneyin
- Basit sorulardan başlayıp kademeli olarak zor sorulara geçin
- Çözümlerinizi adım adım yazarak ilerleyin
Konuyu tam olarak kavramak için günde 15-20 dakika düzenli pratik yapmanızı öneririm. Zamanla bu ilişkileri daha net görmeye başlayacaksınız.
Merkez Açısı ve Çevre Açısı
Merkez açısı ve çevre açısı arasındaki ilişkiyi anlamak için öncelikle bu iki açının tanımlarını netleştirmek faydalı olacaktır. Merkez açısı, çemberin merkezinden geçen iki yarı çapın oluşturduğu açıdır ve bu açının ölçüsü, gördüğü yay uzunluğuna eşittir. Yani, merkez açısı ne kadar büyükse, gördüğü yay da o kadar uzundur.
Çevre açısı ise, çemberin dışındaki bir noktadan çembere çizilen iki kenarın oluşturduğu açıdır. Çevre açısı, gördüğü yay uzunluğunun yarısı kadardır. Bu nedenle, merkez açısının ölçüsü çevre açısının ölçüsünden iki kat daha fazladır. Örneğin, eğer bir merkez açısı 60 derece ise, bu durumda ona karşılık gelen çevre açısı 30 derece olur.
Yay Açısı Hesaplama Örnekleri
Yay açısı hesaplamak için birkaç temel formül ve örnekle pratik yapabilirsiniz:
1. Merkez Açısı Hesaplama: Eğer çemberin yarıçapı \( r \) ve yay uzunluğu \( L \) ise, merkez açısını (radyan cinsinden) şu formülle bulabilirsiniz:
\[ \theta = \frac{L}{r} \]
Burada \( \theta \), yay uzunluğu ile yarıçap arasındaki orandır.
2. Çevre Açısı Hesaplama: Yukarıdaki formülden yola çıkarak, çevre açısını hesaplamak için:
\[ \text{Çevre Açısı} = \frac{\theta}{2} \]
Örneklerle Pratik Yapma
Farklı yay uzunlukları ve yarıçaplar ile pratik yaparak bu kavramları pekiştirebilirsiniz. Örneğin:
- Yarıçapı 5 cm olan bir çemberde, yay uzunluğu 10 cm ise merkez açısını hesaplayın. Sonra bu açının yarısını alarak çevre açısını bulun.
- Yatay bir çemberde farklı yay uzunlukları vererek, merkez ve çevre açılarını karşılaştıran sorular oluşturabilirsiniz.
Bu tür alıştırmalar, konuyu daha iyi anlamanıza ve pratik yapmanıza yardımcı olacaktır. Herhangi bir konuda daha fazla yardıma ihtiyacınız olursa, sormaktan çekinmeyin.
Bu yazıda çemberde açılar ve açılara ait formüller hakkında oldukça detaylı bilgiler verilmiş. Merkez açı, çevre açı ve iç açı gibi farklı açı türlerinin tanımları ve hesaplama yöntemleri net bir şekilde açıklanmış. Özellikle merkez açının gördüğü yay uzunluğuna eşit olduğu ve çevre açısının ise gördüğü yay uzunluğunun yarısı kadar olduğu bilgisi önemli. Çemberde açılar ile ilgili formüllerin yanı sıra, dış açı ve teğet-kiriş açısı gibi diğer önemli kavramlar da ele alınmış. Merkez açı ile çevre açısı arasındaki oran ile ilgili olarak, merkez açının iki katı kadar çevre açısının olması durumu da çok önemli. Çemberdeki bu açılarla ilgili formüllerin ve oranların anlaşılması, geometri derslerinde ve problemlerde büyük kolaylık sağlayacaktır. Peki, çemberdeki açılarla ilgili daha fazla açılardan birinin formülünü ve hesaplama yöntemini öğrenmek ister misin?
Değerli Tuhfe Bey, çemberdeki açılar konusundaki detaylı yorumunuz için teşekkür ederim. Çember geometrisinde en önemli açı türlerinden biri olan teğet-kiriş açısının formülü ve hesaplama yöntemi şöyledir:
Teğet-Kiriş Açısı Formülü:
- Teğet-kiriş açısı, gördüğü yayın ölçüsünün yarısına eşittir
- Formül: Teğet-kiriş açısı = Gördüğü yayın ölçüsü ÷ 2
- Hesaplama: Örneğin, teğet-kiriş açısının gördüğü yay 80° ise, açı = 80° ÷ 2 = 40° olur
Bu açı, çembere bir noktada değen teğet ile çemberi iki noktada kesen kirişin oluşturduğu açıdır ve çevre açı ile benzer özellik gösterir.
Değerli Tuhfe Bey, çemberdeki açılar konusundaki detaylı incelemeniz gerçekten takdire şayan. Çember geometrisinde en çok merak edilen konulardan biri olan teğet-kiriş açısının formülü ve hesaplama yöntemi şöyledir:
Teğet-Kiriş Açısı Formülü:
Teğet-kiriş açısı, gördüğü yayın ölçüsünün yarısına eşittir. Matematiksel olarak ifade edersek:
- Açı = Gördüğü yayın ölçüsü / 2
Hesaplama Yöntemi:
1. Teğet ile kirişin kesiştiği noktayı belirleyin
2. Bu açının gördüğü yayın ölçüsünü bulun
3. Yay ölçüsünü 2'ye bölün
Örneğin, teğet-kiriş açısının gördüğü yay 80° ise, açının ölçüsü 80/2 = 40° olacaktır. Bu açı türü özellikle çemberdeki açı problemlerinde sıklıkla karşımıza çıkar ve diğer açı türleriyle olan ilişkisini anlamak problem çözmede büyük avantaj sağlar.
Merhaba Tuhfe,
Yazınızda çemberdeki açılarla ilgili verdiğiniz detaylı bilgiler gerçekten çok faydalı. Merkez Açısı ve Çevre Açısı arasındaki ilişkiyi vurgulamanız, bu kavramların daha iyi anlaşılmasına yardımcı oluyor. Özellikle merkez açısının gördüğü yay uzunluğuna eşit olması ve çevre açısının bunun yarısı kadar olması, öğrencilerin geometri derslerinde sıkça karşılaşacakları önemli bir bilgi.
Ayrıca, Dış Açılar ve Teğet-Kiriş Açısı gibi ilave konuları da ele almanız, çemberle ilgili daha kapsamlı bir anlayış sunuyor. Merkez açısının iki katı olan çevre açısının olması durumu da oldukça kritik bir nokta. Bu tür formüller ve oranlar, geometri problemlerin çözümünde büyük kolaylık sağlayacaktır.
Elbette, çemberdeki açılarla ilgili daha fazla açıdan birinin formülünü ve hesaplama yöntemini öğrenmek isterim. Bu tür bilgiler, hem öğretim açısından hem de pratik uygulamalar için oldukça değerlidir. Teşekkür ederim!
Bu çember üzerindeki açı türlerini nasıl daha iyi anlayabilirim? Özellikle teğet-kiriş açısı ve iç açı arasındaki farkı karıştırıyorum. Yardımcı olabilir misiniz?
Tabii Mahinur Hanım, çemberdeki açı türlerini anlamanıza yardımcı olayım. Özellikle teğet-kiriş açısı ve iç açı arasındaki farkı netleştirelim:
Teğet-Kiriş Açısı:
- Çembere bir noktada değen teğet ile bu noktadan geçen bir kirişin oluşturduğu açıdır
- Bu açının ölçüsü, gördüğü yayın ölçüsünün yarısına eşittir
- Örnek: Çembere A noktasında değen bir teğet ve A'dan geçen bir kirişin oluşturduğu açı
İç Açı:
- Çemberin iç bölgesinde, iki kirişin kesişmesiyle oluşan açıdır
- Bu açının ölçüsü, gördüğü yayların ölçüleri toplamının yarısına eşittir
- Örnek: Çember içinde kesişen iki kirişin oluşturduğu açı
Temel Farklar:
- Teğet-kiriş açısında bir kenar teğettir, iç açıda her iki kenar da kiriştir
- Teğet-kiriş açısı çemberin dışına doğru açılır, iç açı çemberin iç bölgesindedir
- Formülleri farklıdır: teğet-kiriş açısı tek yayın yarısı, iç açı iki yayın toplamının yarısı
Bu konuyu daha iyi anlamak için farklı örnekler çizerek incelemenizi ve her iki açı türü için örnek problemler çözmenizi öneririm.
Tabii Mahinur Hanım, çemberdeki açı türlerini anlamanıza yardımcı olayım:
Teğet-Kiriş Açısı
- Çembere bir noktada değen teğet ile bu noktadan geçen bir kirişin oluşturduğu açıdır.
- Teğetin değme noktası ile kirişin çemberi kestiği diğer nokta arasındaki yayı görür.
- Ölçüsü gördüğü yayın ölçüsünün yarısına eşittir.
İç Açı
- Köşesi çemberin iç bölgesinde olan ve kenarları çemberi kesen açıdır.
- İki kirişin kesişmesiyle oluşur.
- Ölçüsü gördüğü yay ile karşısındaki yayın ölçüleri toplamının yarısına eşittir.
Temel Fark
Teğet-kiriş açısında bir kenar teğet iken, iç açıda her iki kenar da kiriştir. Teğet-kiriş açısı sadece bir yayı görürken, iç açı iki farklı yayla ilişkilidir.
Pratik yapmak için farklı örnekler çizerek her iki açıyı da gösterip ölçülerini hesaplamanızı öneririm.
Merhaba Mahinur,
Açılar ve Türleri konusunda daha iyi bir anlayışa sahip olmak için öncelikle temel kavramları netleştirmek faydalı olacaktır. Çember üzerinde açılar, genellikle merkez açıları, teğet açıları ve iç açıları olarak sınıflandırılır.
Teğet Açısı: Teğet açısı, bir çemberin bir noktasında çembere teğet olan bir doğru ile çemberin merkezinden geçen bir doğru arasındaki açıdır. Teğet açıları, çemberle yalnızca bir noktada kesiştiği için, bu noktada açının büyüklüğü çemberin merkezi ile olan açıyla ilgilidir.
İç Açı: İç açı ise, çemberin iç kısmında yer alan ve çemberin iki noktası arasında oluşturulan açıdır. Bu açı, çemberin merkezinden geçmeyen iki kenar ile oluşturulur. İç açılar, genellikle çemberin içinde yer alan üçgenlerle veya çokgenlerle ilişkilendirilir.
Farkları Anlamak: Teğet açısı, çemberin bir noktasında oluşurken, iç açı çemberin iç kısmında, yani çemberin sınırları içinde yer alır. Bu iki açının oluşum noktaları ve konumları farklıdır. Bu nedenle, bir çember üzerinde çalışırken bu açıların özelliklerini ve konumlarını görselleştirmek, aralarındaki farkı anlamanıza yardımcı olacaktır.
Bu konuyu daha iyi kavrayabilmek için çember üzerinde çizimler yaparak pratik yapmanız önerilir. Gerekirse bir öğretmen veya eğitmenle çalışarak, bu açıların matematiksel formüllerini ve özelliklerini de öğrenebilirsiniz.
Umarım bu bilgiler yardımcı olur!
- 01 Ekim 2024 Salı
Sabun Formülü Nedir?- 01 Ekim 2024 Salı
10 Sınıf Fizik Formülleri Nelerdir?- 28 Eylül 2024 Cumartesi
Devirli Ondalık Sayılar Formülü- 22 Eylül 2024 Pazar
Eşkenar Üçgen Alan Formülü Nelerdir?- 22 Eylül 2024 Pazar
Tazminat Hesaplama Formülü- 26 Eylül 2024 Perşembe
9 Sınıf Fizik Formülleri Nelerdir?- 29 Eylül 2024 Pazar
9 Sınıf Matematik Formülleri- 22 Eylül 2024 Pazar
Karekök Formülleri Nelerdir?- 21 Eylül 2024 Cumartesi
İvme Formülü Nedir?- 23 Eylül 2024 Pazartesi
Toluen Formülü Nelerdir?- 28 Eylül 2024 Cumartesi
Fosfit Formülü Nedir?- 23 Eylül 2024 Pazartesi
Çamaşır Suyu Formülü Nedir?- 28 Eylül 2024 Cumartesi
Çemberde Açı Formülleri Nelerdir?- 25 Eylül 2024 Çarşamba
Dikromat Formülü Nelerdir?- 21 Eylül 2024 Cumartesi
Dörtgen Formülleri Nelerdir?- 28 Eylül 2024 Cumartesi
Sodyum Fosfat Formülü Sodyum Fosfat Çeşitleri- 21 Eylül 2024 Cumartesi
Toplam Formülleri Çeşitleri- 20 Eylül 2024 Cuma
Glikol Formülü Nedir?- 23 Eylül 2024 Pazartesi
Kalsiyum Nitrat Formülü Nedir?- 23 Eylül 2024 Pazartesi
Excelde Formül Yazma- 22 Eylül 2024 Pazar
10 Sınıf Geometri Formülleri- 28 Eylül 2024 Cumartesi
Kürenin Yüzey Alanı Formülü Nelerdir?- 25 Eylül 2024 Çarşamba
Saç Çıkarma Formülü- 23 Eylül 2024 Pazartesi
11 Sınıf Fizik Formülleri Nelerdir?- 28 Eylül 2024 Cumartesi
Sinüs Alan Formülü Nelerdir?- 23 Eylül 2024 Pazartesi
Daire Formülleri Nelerdir?- 28 Eylül 2024 Cumartesi
Fizik Hız Formülleri Nelerdir?- 22 Eylül 2024 Pazar
Köşegen Sayısı Formülü- 22 Eylül 2024 Pazar
Özdeşlik Formülleri Nelerdir?- 03 Ekim 2024 Perşembe
Standart Sapma Formülü- 22 Eylül 2024 Pazar
Zeka Küpü Formülü Nasıl Çözülür?- 01 Ekim 2024 Salı
Fizik Atış Formülleri Nelerdir?