
Dörtgen Formülleri Nelerdir?
Dörtgenler, geometrinin temel yapı taşlarından biridir ve çeşitli türleri ile farklı özellikler taşır. Bu içerikte, kare, dikdörtgen, paralelkenar, trapez ve yamuk gibi dörtgen türlerinin formülleri ve özellikleri detaylandırılmaktadır. Geometrik problemleri çözmek için bu bilgilerin önemi büyüktür.
Dörtgen, geometrinin temel şekillerinden biridir ve dört kenarı, dört açısı bulunur. Dörtgenler, birçok farklı türe ayrılabilir; kare, dikdörtgen, paralelkenar, trapez ve yamuk gibi. Bu makalede, dörtgenlerin çeşitli türleri ve bu türler için kullanılan formüller detaylandırılacaktır. Dörtgen Türleri ve Özellikleri Dörtgenler, kenar uzunlukları ve açıları bakımından farklılık gösterir. Aşağıda çeşitli dörtgen türleri ve özellikleri açıklanmaktadır:
Kare Formülü Kare, tüm kenar uzunluklarının eşit olduğu özel bir dörtgendir. Kare için alan ve çevre hesaplama formülleri şöyledir:- Alan (A) = Kenar uzunluğu (a) x Kenar uzunluğu (a)- Çevre (C) = 4 x Kenar uzunluğu (a) Dikdörtgen Formülü Dikdörtgen, karşılıklı kenarları eşit olan ve tüm açıları 90 derece olan bir dörtgendir. Dikdörtgenin alan ve çevresi şu şekilde hesaplanır:- Alan (A) = Uzun kenar (l) x Kısa kenar (w)- Çevre (C) = 2 x (Uzun kenar (l) + Kısa kenar (w)) Paralelkenar Formülü Paralelkenar, karşılıklı kenarları eşit ve paralel olan bir dörtgendir. Paralelkenarın alanı, yükseklik ile tabanın çarpımıyla hesaplanır:- Alan (A) = Taban (b) x Yükseklik (h)- Çevre (C) = 2 x (Kenar 1 (a) + Kenar 2 (b)) Trapez Formülü Trapez, bir çift karşıt kenarı paralel olan bir dörtgendir. Trapezin alanı, üst ve alt taban ile yükseklik arasındaki ilişki ile hesaplanır:- Alan (A) = (Üst taban (a) + Alt taban (b)) x Yükseklik (h) / 2- Çevre (C) = Üst kenar + Alt kenar + Yan kenar 1 + Yan kenar 2 Yamuk Formülü Yamuk, iki kenarı paralel olan dörtgenlerdir. Aşağıda bu dörtgenin alanı hesaplanır:- Alan (A) = (Taban 1 (a) + Taban 2 (b)) x Yükseklik (h) / 2- Çevre (C) = Taban 1 + Taban 2 + Yan kenar 1 + Yan kenar 2 Sonuç Dörtgenler, temel geometrik şekiller arasında önemli bir yere sahiptir. Farklı dörtgen türlerinin özellikleri ve formülleri, matematiksel problemleri çözmek için kritik öneme sahiptir. Dörtgenlerin alan ve çevre formüllerinin doğru bir şekilde kullanılması, geometri derslerinde ve pratik uygulamalarda büyük fayda sağlar. Ekstra Bilgiler - Dörtgenlerin iç açıları toplamı her zaman 360 derecedir.- Dörtgenler, simetrik özellikleri ve düzgün dörtgenler olarak sınıflandırılabilir.- Geometrik şekillerin görselleştirilmesi, dörtgenlerin anlaşılmasını kolaylaştırır. Bu bilgiler, dörtgenlerin geometrik özellikleri ve formülleri hakkında kapsamlı bir anlayış sunmaktadır. Geometri alanında daha fazla bilgi edinmek için çeşitli kaynaklar ve kitaplar incelenebilir. |
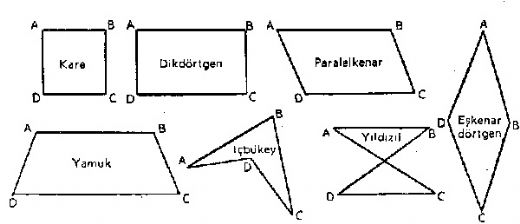















































Dörtgenler hakkında verilen bilgiler oldukça faydalı. Özellikle dikdörtgen, kare, eşkenar dörtgen ve paralelkenar için alan ve çevre formüllerinin net bir şekilde yazılması, matematiksel hesaplamalarda çok yardımcı oluyor. Kendi deneyimlerimden biliyorum ki, bu formülleri doğru bir şekilde kullanmak, geometri derslerinde başarı sağlamanın anahtarı. Sizce de bu formülleri öğrenmek ve pratik yapmak, matematikteki temel becerilerden biri değil mi?
Merhaba Devrim,
Yorumunuz için teşekkürler. Gerçekten de dörtgenlerin alan ve çevre formüllerini öğrenmek, geometri derslerinde büyük bir avantaj sağlıyor. Bu formüller, geometri problemlerini çözme yeteneğimizi geliştiriyor ve matematiksel düşünme becerimizi artırıyor. Pratik yapmak, formülleri anlamayı ve uygulamayı pekiştiriyor, bu da matematikteki temel becerilerden biri olarak kabul ediliyor. Ayrıca, bu bilgilerin günlük yaşamda da ne kadar işlevsel olduğunu görmek, matematiğe olan ilgiyi artırıyor. Sizce, bu formülleri günlük hayatta nasıl kullanabiliriz?