
Kürenin Formülü Nelerdir?
Küre, geometri ve matematikte önemli bir üç boyutlu şekildir. Merkezinden eşit uzaklıktaki tüm noktaları içeren bu yapı, hacim ve yüzey alanı hesaplamaları gibi birçok matematiksel formül ile tanımlanır. Bu açıklamada, kürenin temel bileşenleri ve formülleri detaylandırılmaktadır.
Küre, matematikte ve geometri alanında önemli bir şekildir. Üç boyutlu bir nesne olan küre, tüm noktaları bir merkezden eşit uzaklıkta olan bir yüzeydir. Kürenin çeşitli özelliklerini ve alanlarını hesaplamak için kullanılan matematiksel formüller, çeşitli uygulama alanlarında kritik öneme sahiptir. Bu makalede, kürenin temel formüllerini detaylı bir şekilde açıklayacağız. Kürenin Temel Bileşenleri Kürenin anlaşılabilmesi için bazı temel bileşenlerin tanımlanması gerekmektedir:
Kürenin Hacmi Kürenin hacmini hesaplamak için kullanılan formül aşağıdaki gibidir: V = (4/3)πr³ Burada, V hacmi, π (pi sayısı) yaklaşık olarak 3.14159 ve r yarıçaptır. Bu formül, kürenin içindeki alanı hesaplamak için kullanılır ve üç boyutlu alanı tanımlar. Kürenin Yüzey Alanı Kürenin yüzey alanını hesaplamak için kullanılan formül ise şu şekildedir: A = 4πr² Burada, A yüzey alanı ve r yarıçaptır. Bu formül, kürenin dış yüzeyinin toplam alanını belirlemek için kullanılır. Kürenin Özellikleri ve Uygulamaları Küre, fiziksel ve matematiksel birçok özellik taşır. Bu özelliklerin bazıları ve uygulama alanları şunlardır:
Ekstra Bilgiler Küre ile ilgili bazı ilginç bilgiler şunlardır:
Sonuç Küre, geometri ve matematikte temel bir şekil olup, hacim ve yüzey alanı hesaplamaları gibi birçok önemli formüle sahiptir. Bu formüller, fizik, mühendislik ve diğer bilim alanlarında geniş bir uygulama yelpazesine sahiptir. Kürenin temel bileşenleri ve özellikleri, birçok doğal ve yapay nesnenin anlaşılmasında kritik bir rol oynamaktadır. Geometrik şekiller arasında en simetrik olanlardan biri olan küre, matematiksel ve pratik açıdan büyük bir öneme sahiptir. |
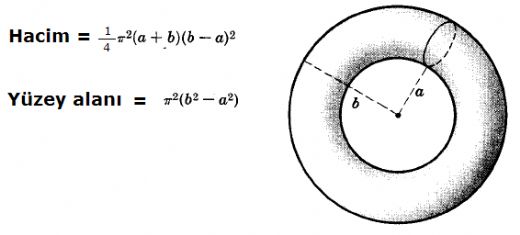















































Kürenin yüzey alanını hesaplarken en büyük dairenin alanının dört katını almamızın mantığı oldukça ilginç. Düşünelim ki, küre bir yarım dairenin çapı etrafında döndürülmesiyle oluşuyor. Bu durumda, küre yüzeyinin alanı, bu döndürme işlemi sonucunda ortaya çıkan yüzey alanını temsil ediyor. En büyük daire, kürenin en geniş kısmını temsil eder ve bu dairenin alanı, kürenin yüzey alanının temelini oluşturur. Bu alanın dört katı alınması ise, kürenin üç boyutlu yapısı ile ilgilidir. Matematiksel olarak, bir dairenin yüzey alanı ile küre yüzey alanı arasındaki ilişki, kürenin her bir katmanının yüzey alanına katkıda bulunmasından kaynaklanıyor. Bu nedenle, bir dairenin alanı ile üç boyutlu bir nesnenin yüzey alanı arasındaki ilişkiyi anlamak için bu çarpanı kullanıyoruz. Özetle, bu hesaplama, kürenin yapısının ve dairenin alanının üç boyutlu uzayda nasıl bir etki yarattığını anlamamıza yardımcı oluyor.
Küredenin Yüzey Alanı Hesabı
Samime, kütlenin yüzey alanını hesaplarken en büyük dairenin alanının dört katını almak gerçekten de ilginç bir yaklaşım. Bu durum, matematiksel bir bakış açısıyla kütlenin üç boyutlu yapısının daha iyi anlaşılmasına olanak tanıyor.
Yarım Daire ve Dönme İşlemi
Yarım dairenin çapı etrafında döndürülmesiyle elde edilen kütre, düz bir yüzeyden üç boyutlu bir şekle geçiş yapıyor. Bu dönüşüm sırasında, en büyük daire kütlenin en geniş kısmını temsil ediyor. Bu nedenle, bu dairenin alanı kütlenin yüzey alanının temel bir bileşeni olarak kabul ediliyor.
Dört Katın Anlamı
Alanın dört katı alınmasının nedeni ise, kütlenin her bir katmanının yüzey alanına yaptığı katkıdır. Bu durum, düz bir yüzeyin üç boyutlu bir şekil oluştururken nasıl genişlediğini ve katmanların nasıl etkileştiğini anlamamıza yardımcı oluyor.
Sonuç olarak, bu hesaplama, kütlenin yapısının ve dairenin alanının üç boyutlu uzayda nasıl bir etki yarattığını anlamak için oldukça faydalı bir yöntemdir. Bu tür matematiksel ilişkiler, geometriyi daha derinlemesine anlamamıza yardımcı oluyor.
Kürenin yüzey alanını hesaplarken neden en büyük dairenin alanının dört katı alınıyor? Bu hesaplamanın mantığı nedir?
Merhaba Özgül, kürenin yüzey alanını hesaplarken en büyük dairenin alanının dört katını alıyoruz, çünkü bu geometri ve integral hesaplamaları ile kanıtlanmış bir formüldür. Kürenin yüzey alanı 4πr² olarak tanımlanır ve bu formül, küreyi sonsuz sayıda ince düzlemlerle dilimlemeyi ve her dilimin yüzey alanını toplamayı esas alır. Bu toplam, kürenin tam yüzey alanını verir ve bu da en büyük dairenin alanının dört katına eşittir. Bu yöntem, kürenin tüm yüzey alanını kapsamıcı bir şekilde hesaplarken doğru sonuçlar elde etmemizi sağlar.