Dik Yamuk Alan Formülü Nelerdir?

Dik yamuk, iki tabanı paralel olan ve yüsekliğiyle tanımlanan bir geometrik şekildir. Alanı, alt ve üst taban uzunlukları ile yükseklik kullanılarak hesaplanır. Bu yazıda, dik yamuk alan formülü ve örnek uygulamalarına dair bilgiler sunulmaktadır.

Konu kakkında 1 soru soruldu ve cevaplandı

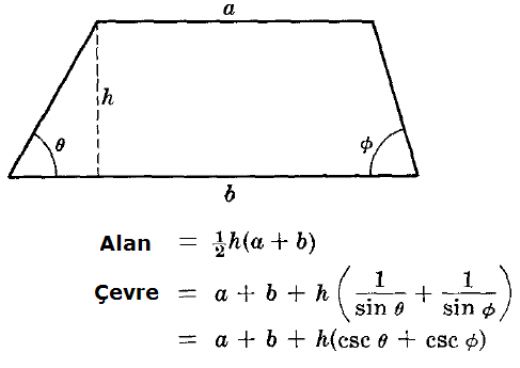
Dik Yamuk Alan Formülü Nedir?

Dik yamuk, bir tabanı ve bir üst kenarı bulunan, iki kenarının ise paralel olduğu bir dörtgendir. Dik yamuk, iki tabanına dik olan yükseklikle tanımlanır. Bu geometrik şeklin alanını hesaplamak için kullanılan formül, matematiksel olarak oldukça basittir.

Dik Yamuk Alan Formülü

Dik yamuk alanı, taban uzunlukları (a ve b) ile yükseklik (h) kullanılarak şu formülle hesaplanır:\[ \text{Alan} = \frac{(a + b) \cdot h}{2} \]Burada:- \( a \): Alt tabanın uzunluğu- \( b \): Üst tabanın uzunluğu- \( h \): Yükseklik

Örnek Uygulamalar

Dik yamuk alan formülünü daha iyi anlamak için birkaç örnek üzerinden gidebiliriz.

Örnek 1: Alt tabanı 8 cm, üst tabanı 5 cm ve yüksekliği 4 cm olan bir dik yamuk için alan hesaplayalım.\[ \text{Alan} = \frac{(8 + 5) \cdot 4}{2} = \frac{13 \cdot 4}{2} = \frac{52}{2} = 26 \, \text{cm}^2 \]
Örnek 2: Alt tabanı 10 cm, üst tabanı 6 cm ve yüksekliği 3 cm olan bir dik yamuk için alan hesaplayalım.\[ \text{Alan} = \frac{(10 + 6) \cdot 3}{2} = \frac{16 \cdot 3}{2} = \frac{48}{2} = 24 \, \text{cm}^2 \]

Dik Yamuk ile İlgili Başka Kavramlar

Dik yamuk, çeşitli alanlarda kullanılmakta olup, bu geometrik şekil ile ilgili bazı önemli kavramlar şunlardır:

Tabanlar: Dik yamukta iki paralel kenar bulunur ve bunlara taban denir.
Yükseklik: Tabanlar arasındaki dik mesafedir.
Kenarlar: Tabanlar dışında kalan diğer iki kenar, yan kenarlardır.
Dik Yamuk Alanı: Yukarıda belirtilen formülle hesaplanır.

Dik Yamuk Alanının Kullanım Alanları

Dik yamuk alan formülü, birçok alanda uygulama bulmaktadır. Bunlar arasında:

Mimari Tasarım: Binaların ve yapıların tasarımında dik yamuk alan hesaplamaları önemli bir yer tutar.
İnşaat Mühendisliği: Arazi ölçümlerinde dik yamuk alan hesapları kullanılır.
Eğitim: Matematik derslerinde geometri konularında sıkça kullanılmaktadır.

Sonuç

Dik yamuk, geometrik şekiller arasında önemli bir yere sahiptir ve alanının hesaplanması, çeşitli uygulamalarda kritik bir öneme sahiptir. Yukarıda verilen formül ve örnekler, dik yamuk alanının nasıl hesaplanacağını anlamak için bir temel sağlamaktadır. Matematiksel kavramların doğru bir şekilde anlaşılması, mühendislikten mimariye birçok alanda başarıyı artırmaktadır.

Ek olarak, dik yamuk ile ilgili daha derinlemesine bilgi edinmek isteyenler için çeşitli akademik kaynaklar ve geometri kitapları önerilmektedir. Bu kaynaklar, öğrencilerin ve profesyonellerin dik yamuk ve diğer geometrik şekiller hakkında daha fazla bilgi edinmelerine yardımcı olacaktır.

Yeni Soru Sor / Yorum Yap

Sizden Gelen Sorular / Yorumlar

Temel 12 Temmuz 2024 Cuma

Bir dik yamuk problemi çözerken yüksekliği bulmak için alt taban ile üst tabanı çarpmak gerektiğinde, neden bu işlemin karesini alıyoruz? Bu karesi alınan ifade neyi temsil ediyor ve neden yüksekliği hesaplarken kullanıyoruz?

Admin 12 Temmuz 2024 Cuma

Temel, dik yamuk problemlerinde yüksekliği bulurken alt taban ile üst tabanı çarpmıyoruz. Yüksekliği bulmak için genellikle Pisagor teoremi veya trigonometri kullanılır. Alt taban ile üst tabanı çarpmak ve bu işlemin karesini almak gibi bir adım geometri kurallarına uygun değildir.

Eğer bir dik yamukta yüksekliği bulmak istiyorsak, yamukta dik olan kenarı ve yamuk tabanlarının uzunluklarını kullanarak, gerekli durumlarda Pisagor teoremi uygulanır. Yani, yüksekliği bulmak için alt taban ile üst tabanı çarpmak ve bu işlemin karesini almak yanlış bir yaklaşımdır. Umarım bu açıklama senin için faydalı olmuştur.