
Karekök Formülleri Nelerdir?
Karekök, matematiksel işlemlerde önemli bir yer tutar ve çeşitli formüller aracılığıyla ifade edilir. Bu yazıda, karekökün tanımı, temel formülleri ve kullanım alanları detaylı bir şekilde ele alınarak, matematiksel hesaplamalarda nasıl bir rol oynadığı açıklanmaktadır.
Karekök, matematikte bir sayının kendisi ile çarpıldığında belirli bir değeri veren bir sayıdır. Örneğin, 4 sayısının karekökü 2'dir, çünkü 2 x 2 = 4. Karekök işlemleri, birçok matematiksel probleme çözüm bulmak için kullanılır ve çeşitli formüller aracılığıyla ifade edilebilir. Bu makalede, karekök formüllerini ve bunların kullanım alanlarını detaylı bir şekilde inceleyeceğiz. Karekök Nedir?Karekök, matematikte bir sayının, kendisi ile çarpıldığında belirli bir sayıyı veren pozitif bir sayı olarak tanımlanır. Karekök sembolü "√" ile gösterilir. Örneğin, √9 = 3, çünkü 3 x 3 = 9. Karekök, genellikle üç ana kategoride incelenir:
Karekök Formülleri Karekök ile ilgili bazı temel formüller şunlardır:
Karekök Kullanım Alanları Karekök, matematiğin çeşitli alanlarında önemli bir yere sahiptir. Başlıca kullanım alanları şunlardır:
Karekök İşlemleri ve Özellikleri Karekök işlemleri, genellikle aşağıdaki özelliklere sahiptir:
Sonuç Karekök formülleri, matematik ve uygulamalı bilimlerde önemli bir yere sahiptir. Bu formüller, çeşitli hesaplamalarda ve problem çözme süreçlerinde etkin bir şekilde kullanılmaktadır. Karekök işlemlerinin temel özelliklerini ve kullanım alanlarını anlamak, matematiksel becerilerin geliştirilmesi açısından oldukça önemlidir. Matematiksel düşünme yeteneğini artırmak ve çeşitli alanlarda uygulamalarını keşfetmek için karekök formüllerine hakim olmak gerekmektedir. |
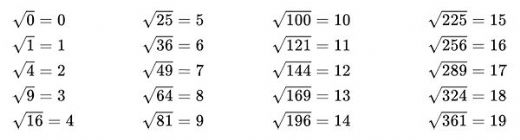















































Karekök formülleri hakkında daha fazla bilgi almak için, a kök b şeklinde yazma işlemlerinin nasıl yapıldığını merak ediyorum. Özellikle, karekök içindeki sayıları asal çarpanlarına ayırmanın avantajları nelerdir? Bu yöntemle ne tür örnekler verebilirsiniz?
Karekök Formülleri ve İşlemleri
Karekök, bir sayının kendisiyle çarpıldığında belirli bir değeri veren sayıyı ifade eder. Örneğin, √a ifadesi, a sayısının karekökünü temsil eder. Karekök işlemlerinin temel özelliklerinden biri, karekök içinde bulunan sayıları asal çarpanlarına ayırarak daha basit hale getirmektir.
Asal Çarpanlara Ayırmanın Avantajları
Karekök içerisindeki sayıları asal çarpanlarına ayırmanın birçok avantajı vardır. Öncelikle, bu işlem sayesinde karekök içerisindeki değerleri daha kolay sadeleştirebiliriz. Asal çarpanlar, sayının yapı taşlarıdır; bu nedenle, bir sayının asal çarpanlarını bilmek, onu daha anlamlı ve yönetilebilir bir şekilde ifade etmemizi sağlar. Örneğin, √36 işlemi yapılırken 36 sayısını asal çarpanlarına ayırdığımızda 36 = 2² × 3² olduğunu görebiliriz. Bu durumda √36 = 6 olarak kolayca hesaplanabilir.
Örnekler
1. √50 işlemi:
- 50 sayısını asal çarpanlarına ayırıyoruz: 50 = 2 × 5².
- Karekök işlemi: √50 = √(2 × 5²) = √2 × √(5²) = √2 × 5 = 5√2.
2. √72 işlemi:
- 72 sayısını asal çarpanlarına ayıralım: 72 = 2³ × 3².
- Karekök işlemi: √72 = √(2³ × 3²) = √(2² × 2 × 3²) = √(2²) × √(3²) × √2 = 2 × 3 × √2 = 6√2.
Bu örneklerde görüldüğü gibi, asal çarpanlara ayırmak, karekök işlemlerini daha yönetilebilir hale getirir ve sonucun daha kolay bulunmasını sağlar.
Karekök formüllerini öğrenmek oldukça karmaşık bir süreç gibi geliyor. Özellikle karekök içindeki ifadeleri kök dışına çıkarma işlemi bazen göz korkutucu olabiliyor. Belirttiğiniz gibi, karekök içindeki sayıları çarpanları üzerinden ele alarak, karesi alınabilen sayılarla ayırmak oldukça pratik bir yöntem. Ancak, bu işlemi hızlıca yapabilmek için bazı sayılarının karelerini ezbere bilmek gerçekten faydalı oluyor. Örneğin, karekök içindeki sayının asal çarpanlarına ayrılması gerektiğinde, bunu yapmak için biraz pratik yapmam gerekiyor. Bu tür işlemleri daha hızlı yapabilmek adına, belli başlı sayıların karelerini ezberlemek iyi bir başlangıç olabilir. Karekök içinde karmaşık ifadelerle karşılaştığımda, genelde önce sadeleştirmeyi deniyorum, fakat bazen bu işin içinden çıkamadığım da oluyor. Sonuç olarak, bu tür konularda pratik yapmak ve formülleri daha iyi anlamak, süreci oldukça kolaylaştırıyor. Sizin önerdiğiniz yöntemleri de uygulamaya çalışacağım.
Kareköklere Giriş
Kutan, karekök formlarını öğrenmek başlangıçta karmaşık görünebilir, ancak zamanla pratik yaptıkça daha anlaşılır hale gelecektir. Karekök içindeki ifadeleri kök dışına çıkarma işlemi, gerçekten de bazı temel bilgileri gerektiriyor.
Asal Çarpanlar ve Karekök
Asal çarpanlara ayırma işlemi, karekökleri daha kolay hale getirebilir. Bu konuda pratik yapmaya devam ettikçe hızlanacaksınız. Örneğin, 36 sayısını ele alırsak, asal çarpanları 2 ve 3'tür. 36’nın karekökü 6’dır çünkü 6 x 6 = 36. Bu tür örnekleri sık sık yaparak, sayıların karelerini aklınızda tutmak daha kolay olacaktır.
Sadeleştirme İşlemleri
Karekök içindeki karmaşık ifadeleri sadeleştirmek için belirli adımları izlemek önemlidir. Önce sayıyı asal çarpanlarına ayırarak başlayın, ardından karekök dışına çıkabilecek çarpanları belirleyin. Bu süreçte, pratik yapmak gerçekten büyük bir fark yaratır. Sadeleştirmeyi başaramadığınız durumlarda, kararlı kalıp pes etmemek de önemlidir.
Öneriler
Sonuç olarak, kareköklerle ilgili pratik yapmak ve temel formülleri anlamak, bu konudaki yetkinliğinizi artıracaktır. Önerdiğim yöntemleri uygulayarak, daha fazla alıştırma yapmayı unutmayın. Başarılar dilerim!
Karekök formüllerini anlamakta zorlanıyorum. Örneğin, karekök içindeki ifadeyi kök dışına çıkarma işlemi nasıl daha hızlı yapılabilir?
Murad Bey,
Karekök formüllerini anlamakta zorlanmanız oldukça normal ve birçok kişi bu konuda benzer zorluklar yaşıyor. Karekök içindeki ifadeyi kök dışına çıkarma işlemi için bazı pratik yöntemler ve kurallar vardır. İşte birkaç temel ipucu:
1. Çarpanlara Ayırma: Karekök içindeki sayıyı çarpanlarına ayırarak daha kolay kök dışına çıkarabilirsiniz. Örneğin, √50 ifadesini √(252) olarak yazabilirsiniz. Bu durumda, 25'in karekökü olan 5, kök dışına çıkar ve ifade 5√2 olur.
2. Tam Kare Sayılar: Karekök içindeki tam kare sayıları tanımak işinizi kolaylaştırır. Tam kare olan sayılar (1, 4, 9, 16, 25, 36, 49, 64, 81, 100, vb.) kök dışına daha kolay çıkarılır.
3. Kök Kuralları: Karekök alma işlemlerinde şu temel kuralları hatırlamak önemlidir:
- √(ab) = √a √b
- √(a/b) = √a / √b
4. Pratik Yapma: Matematikte pratik yapmak her zaman önemlidir. Farklı sayılarla bol bol alıştırma yaparak karekök işlemlerine daha fazla aşina olabilirsiniz.
Bu yöntemlerle karekök içindeki ifadeleri daha hızlı ve etkili bir şekilde kök dışına çıkarabilirsiniz. Umarım bu açıklamalar sizin için faydalı olur!
Saygılarımla,