
Koni Formülleri Nelerdir?
Koni, tabanı dairesel olan ve tepe noktasına kadar yüksekliği ölçülebilen üç boyutlu bir geometrik şekildir. Bu yazıda, koninin temel formülleri, yüzey alanı, hacmi, özellikleri ve çeşitli uygulama alanları hakkında bilgi verilmektedir. Koni, mühendislik ve matematikte önemli bir yere sahiptir.
Koni, üç boyutlu bir geometrik şekil olup, tabanı bir daire ve tepe noktasının taban düzlemine olan dik mesafesi ile tanımlanır. Koni, pek çok alanda, özellikle mühendislik, mimarlık ve matematik gibi disiplinlerde önemli bir yere sahiptir. Bu makalede, koni ile ilgili başlıca formüller, özellikler ve uygulama alanları üzerinde durulacaktır. Koni Nedir?Koni, bir dairesel tabana ve bir tepe noktasına sahip olan bir üç boyutlu şekildir. Tabanın merkezi ile tepe noktası arasındaki doğru, koninin yüksekliğini (h) temsil eder. Ayrıca, koninin tabanının yarıçapı (r) ve koninin yüzey alanı ile hacmi gibi önemli ölçümler vardır. Koni Formülleri Koni ile ilgili temel formüller aşağıdaki gibidir:
Koni Yüzey Alanı Koni yüzey alanı, koninin taban alanı ile yan yüzey alanının toplamıdır. Yüzey alanı formülü şu şekildedir:
Burada, A koninin yüzey alanını, r tabanın yarıçapını ve h koninin yüksekliğini temsil eder. Koni yüzey alanı, hem taban alanını hem de yan yüzey alanını içerdiği için, koninin dış yüzeyinin toplam alanını verir. Koni Hacmi Koni hacmi, koninin içindeki üç boyutlu alanı tanımlar ve aşağıdaki formül ile hesaplanır:
Bu formülde, V koninin hacmini, r tabanın yarıçapını ve h koninin yüksekliğini belirtir. Koni hacmi, koninin ne kadar sıvı veya katı madde alabileceğini belirlemek için kullanılır. Koni Özellikleri Koni birçok önemli özelliğe sahiptir:
Koni Uygulamaları Koni, pek çok alanda farklı amaçlarla kullanılmaktadır:
Sonuç Koni formülleri, bu geometrik şeklin hacmi ve yüzey alanı gibi önemli özelliklerini hesaplamak için kritik öneme sahiptir. Koni, birçok bilimsel ve mühendislik uygulamasında önemli bir rol oynar. Geometrik şekillerin temel taşlarından biri olan koni, matematiksel hesaplamalar ve pratik uygulamalar için vazgeçilmezdir. Bu makalede, koni ile ilgili temel bilgileri ve formülleri ele aldık. Koni, hem teorik hem de pratik açıdan önemli bir geometrik şekil olmaya devam etmektedir. |
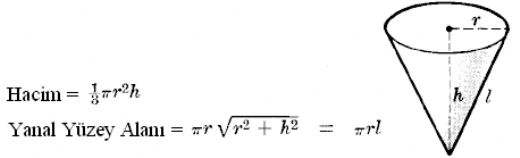















































Koni formüllerini kullanarak koninin yüzey alanı ve hacmini hesaplamaya çalışıyorum ama apotemi uzunluğunu nasıl bulacağımı tam olarak anlayamadım. Bu konuda bir açıklama yapabilir misiniz?
Tabii Asgar, koninin apotem uzunluğunu bulmak için Pythagoras teoremini kullanabilirsin. Koninin dik kesitinde, yükseklik (h), yarıçap (r) ve apotem (a) arasında bir dik üçgen oluşur. Apotem uzunluğu bu üçgenin hipotenüsü olarak kabul edilir. Bu durumda, apotemi şu formülle bulabilirsin:
a = √(r² + h²)
Yani, koninin yarıçapının karesi ile yüksekliğinin karesini topladıktan sonra, bu toplamın karekökünü alarak apotemi bulabilirsin. Bu apotem uzunluğunu kullanarak koninin yanal yüzey alanını hesaplayabilirsin. Umarım bu açıklama işine yarar!