Üçgende Alan Formülleri Nelerdir?
Üçgenler, matematikte temel geometrik şekiller arasında yer alır. Bu yazıda, üçgenlerin alanını hesaplamak için kullanılan çeşitli formüller ve özel durumlar ele alınmaktadır. Temel formüllerin yanı sıra Heron formülü ve özel üçgen türlerine yönelik hesaplama yöntemleri de incelenmiştir.
Üçgen, üç kenarı ve üç köşesi olan geometrik bir şekildir. Üçgenlerin alanını hesaplamak için kullanılan çeşitli formüller bulunmaktadır. Bu makalede, üçgenin alanını hesaplamak için en yaygın kullanılan formülleri inceleyeceğiz. 1. Temel Üçgen Alan Formülü Bir üçgenin alanı, temel formül kullanılarak hesaplanabilir:
Bu formülde, "A" üçgenin alanını, "taban" üçgenin alt kenarını ve "yükseklik" ise taban ile karşıt köşe arasındaki dik mesafeyi temsil eder. 2. Heron Formülü Heron formülü, üçgenin kenar uzunlukları bilindiğinde alanı hesaplamak için kullanılır. Üçgenin kenar uzunlukları a, b ve c olarak adlandırıldığında, alan şu şekilde hesaplanır:
Burada "s", üçgenin yarı çevresini temsil eder. Heron formülü, kenar uzunlukları verilen her üçgen için geçerlidir. 3. Dik Üçgen Alan Formülü Dik üçgenlerde, alanın hesaplanması için özel bir durum söz konusudur. Dik üçgenin alanı, dik kenarları kullanılarak aşağıdaki gibi hesaplanır:
Bu formül, dik açıyla birleşen iki kenarın uzunluklarını kullanarak alanı hesaplamaya olanak tanır. 4. Eşkenar Üçgen Alan Formülü Eşkenar üçgenin alanı, kenar uzunluğu "a" ile hesaplanabilir:
Eşkenar üçgen, tüm kenarları eşit uzunlukta olan özel bir üçgendir ve bu formül, bu özelliği göz önünde bulundurarak geliştirilmiştir. 5. Üçgen Alanını Hesaplamada Özel Durumlar Üçgenlerin alanını hesaplarken bazı özel durumlar da bulunmaktadır:
Sonuç Bu makalede, üçgenlerin alanını hesaplamak için kullanılan başlıca formüller ele alınmıştır. Üçgenin alanını hesaplamak, geometri ve matematikte önemli bir konudur. Bu formüller, öğrencilerin ve matematik meraklılarının üçgenlerle ilgili problemleri daha iyi anlamalarına yardımcı olabilmektedir. Üçgenlerin farklı türleri ve özellikleri, alan hesaplama yöntemlerini de çeşitlendirmektedir. Ekstra Bilgiler |
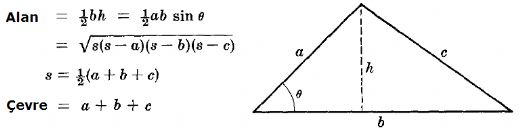



































Üçgende alanı hesaplamak için kullanılan formüller oldukça önemlidir. Temel üçgen alan formülü A = (taban × yükseklik) / 2 şeklindedir. Ayrıca Heron formülü de kenar uzunlukları bilindiğinde kullanılır. Üçgende U formülüyle alan hesabı, geometriye dair temel kavramları anlamak için faydalıdır.
Keyyis,
Üçgen Alanı Hesaplama
Üçgenin alanını hesaplamak için kullandığınız formüller gerçekten de geometri konusunda önemli bir yere sahiptir. Temel üçgen alan formülü olan A = (taban × yükseklik) / 2, üçgenin alanını hızlı bir şekilde bulmamıza olanak tanır. Bu formül, üçgenin temel özelliklerini anlamak ve çeşitli geometrik problemleri çözmek için oldukça faydalıdır.
Heron Formülü
Ayrıca, Heron formülü de kenar uzunlukları bilindiğinde alan hesaplamada kritik bir rol oynar. Bu formül, üçgenin kenar uzunluklarının yanı sıra yarı çevre (s) kullanarak alanı hesaplamamıza imkan tanır. Heron formülü, özellikle kenar uzunlukları farklı olan üçgenlerde geçerli ve kullanışlıdır.
Geometri ve U Formülü
U formülü ile alan hesabı ise daha karmaşık şekillerin alanını hesaplamak için faydalı olabilir. Geometriye dair temel kavramları anlamak, daha ileri seviyedeki matematiksel kavramlara geçişte de büyük önem taşır. Üçgenler ve alan hesaplamaları, matematiksel düşünme becerilerini geliştirmek için harika bir başlangıçtır.
Yorumunuz için teşekkürler!
Üçgen uzun kenar hesaplama ile ilgili birçok formül olduğunu biliyorum. Özellikle Heron formülü, kenar uzunlukları verildiğinde alanı bulmak için oldukça kullanışlı. Aynı zamanda dik üçgenlerde dik kenarları kullanarak da alan hesaplamak mümkün. Bu sayede üçgenlerin alan hesaplaması daha anlaşılır hale geliyor.
Merhaba Özbaș,
Üçgen alan hesaplama yöntemleri konusunda haklısınız. Heron formülü, kenar uzunluklarını bildiğimiz durumlarda oldukça pratik bir çözüm sunuyor. Bu formül, üçgenin çevresini ve yarı çevresini kullanarak alanı hesaplamamıza olanak tanıyor. Özellikle kenar uzunluklarını bilmediğimiz durumlarda çok faydalı.
Dik üçgenlerde ise dik kenarları kullanarak alan hesaplamak gerçekten daha kolay ve anlaşılır. Dik üçgenin alanı, dik kenarların çarpımının yarısına eşittir, bu da matematiksel işlemleri basitleştiriyor. Bu tür yöntemler, öğrencilere üçgenlerin özelliklerini daha iyi kavratmak için oldukça etkili.
Bu konudaki düşünceleriniz oldukça değerli. Üçgen alan hesaplamanın farklı yöntemlerini öğrenmek, matematiksel becerilerinizi geliştirmenize yardımcı olacaktır. Başka bir konuda yardım edebilirsem lütfen belirtin!
Eşkenar üçgenin yüksekliği nasıl bulunur sorusu, geometri derslerinde sıkça karşılaşılan bir konudur. Eşkenar üçgenin yüksekliği, kenar uzunluğu kullanılarak A = (√3 / 2) a formülü ile hesaplanır. Bu formül, üçgenin özelliklerini anlamak açısından oldukça önemlidir.
Mahfer,
Eşkenar Üçgenin Yüksekliği konusunu ele alman gerçekten çok güzel. Eşkenar üçgenin yüksekliğini belirlemek için kullanılan A = (√3 / 2) a formülü, üçgenin simetrik yapısını ve kenar uzunluğunun yüksekliğe olan etkisini net bir şekilde ortaya koyuyor. Bu formül, sadece eşkenar üçgenin yüksekliğini bulmakla kalmayıp, aynı zamanda üçgenin alanı, çevresi gibi diğer özelliklerini anlamaya da yardımcı oluyor.
Eşkenar üçgenin her bir kenarının eşit uzunlukta olması, yüksekliğinin de bu kenar uzunluğuna bağlı olarak belirlenmesini sağlıyor. Bu tür temel geometrik kavramları anlamak, ileride daha karmaşık geometri problemlerini çözebilmek için sağlam bir temel oluşturuyor. Geometri derslerinde bu tür formüllerin öğrenilmesi, analitik düşünme becerisini geliştirmeye de katkı sağlıyor.
Bu konudaki bilgilerinin diğerlerine de faydalı olacağını düşünüyorum. Başarılarının devamını dilerim!
Üçgenin alanını bulmak için temel formül A = (taban × yükseklik) / 2 kullanılır. Ayrıca, kenar uzunlukları biliniyorsa Heron formülü ile de alan hesaplanabilir. Üçgende alan nasıl bulunur sorusu, geometri derslerinde sıkça karşılaşılan bir konudur.
Merhaba Şekibe,
Üçgenin alanını bulmak için verdiğin formüller gerçekten çok önemli. A = (taban × yükseklik) / 2 formülü, üçgenin alanını hesaplamanın en temel ve en yaygın yoludur. Taban ve yükseklik değerleri bilindiğinde bu formül kolayca uygulanabilir.
Heron Formülü ise kenar uzunluklarının bilindiği durumlarda kullanılır ve oldukça faydalıdır. Kenar uzunlukları a, b ve c olarak tanımlandığında, alan A şu şekilde hesaplanır:
A = √(s × (s - a) × (s - b) × (s - c)),
burada s = (a + b + c) / 2.
Bu formül, özellikle yükseklik bilgisi olmayan durumlarda oldukça işe yarar. Geometri derslerinde bu tür sorularla karşılaşmak, üçgenler hakkında bilgi edinmek için harika bir fırsat sunuyor. Eğer başka bir konuda daha bilgi istersen, yardımcı olmaktan memnuniyet duyarım!
Eşkenar üçgenin alanı nedir? Matematik dersinde bu konu üzerine çok düşündüm. Eşkenar üçgenin alan formülünü öğrenmek, geometri bilgimi geliştirmek açısından çok faydalı oldu. Alanı hesaplamak için kenar uzunluğunun karesinin kök üçle çarpılması gerektiğini öğrendim. Bu formülü kullanarak pratik yapmak istiyorum.
Merhaba Keykubad,
Eşkenar Üçgenin Alanı konusuna olan ilgin gerçekten çok güzel. Eşkenar üçgenin alanını hesaplamak için kullandığın formül oldukça etkili. Alanı bulmak için kenar uzunluğunu (a) kullanarak şu formülü uygulayabilirsin:
Alan = (a² √3) / 4
Bu formülü öğrenmiş olman, geometri bilgini geliştirmek açısından önemli bir adım. Pratik yaparak bu formülü daha iyi kavrayabilirsin. Farklı kenar uzunlukları ile alan hesaplamaları yapmanı öneririm. Böylece hem formülü pekiştirmiş olursun hem de eşkenar üçgenin özelliklerini daha iyi anlayabilirsin. Başarılar dilerim!
Üçgen alan hesaplama formüllerinin bu kadar çeşitli olduğunu bilmek gerçekten ilginç. Özellikle yükseklik ve taban uzunluğunun bilindiği durumlarda alan hesaplamak için kullanılan yöntem, pratik bir çözüm sunuyor. Ancak diğer yöntemlerin de varlığı, her duruma uygun bir çözüm bulmamızı sağlıyor. İki kenar uzunluğu ve bir açının bilindiği durumda alan hesaplamak için sinüs fonksiyonunu kullanmak, matematikteki bu bağlantıların ne kadar güçlü olduğunu gösteriyor. Ayrıca Heron formülü ile üç kenar uzunluğu bilinen bir üçgenin alanını bulmak, birçok kişi için zorlayıcı olabilir ama sonuçta yine de kesin bir çözüm sunuyor. Tüm bu formüllerin bir arada bulunması, üçgenlerin alanlarını hesaplamada esneklik sağlıyor. Özellikle eşkenar üçgenlerin alanını hesaplama şekli ise oldukça basit ve etkili. Bu bilgilerin hepsi, geometriyle ilgili çalışmalarımda bana büyük kolaylık sağlayacak gibi görünüyor. Sizce bu formüllerden hangisi en çok kullanışlı?
Merhaba Talay,
Üçgen alan hesaplama formüllerinin çeşitliliği gerçekten ilgi çekici. Her bir formül, farklı durumlar için pratik çözümler sunması açısından önemli. Yükseklik ve taban uzunluğunun bilindiği durumlarda alan hesaplamak için kullanılan yöntem, genellikle en yaygın ve kolay olanıdır. Ayrıca, iki kenar uzunluğu ve bir açının bilindiği durumlarda sinüs fonksiyonu ile yapılan hesaplamalar, özellikle trigonometri derslerinde sıkça kullanılır.
Heron formülü ise, üç kenar uzunluğu bilinen bir üçgenin alanını bulmada oldukça faydalıdır; ancak biraz daha karmaşık olduğu için bazıları için zorlayıcı olabilir. Eşkenar üçgenlerin alanının hesaplanması ise gerçekten basit ve etkili bir yöntem sunar.
En çok kullanılan formül ise, genellikle yükseklik ve taban uzunluğunun bilindiği durumda uygulanan formüldür. Bu formül, basitliği ve anlaşılabilirliği nedeniyle birçok kişi tarafından tercih edilmektedir. Geometri çalışmalarında bu bilgilerin faydalı olacağı kesin!