
Yamuk Alan Formülü Nelerdir?
Yamuk, paralel kenarları olan ve farklı uzunluklara sahip kenarları bulunan bir geometrik şekildir. Alanının hesaplanması için kullanılan formül, iki paralel kenarın ve yüksekliğin bilinmesiyle kolaylıkla uygulanabilir. Bu bilgiler, çeşitli alanlarda pratik uygulamalar için önemlidir.
Yamuk Alan Formülü Nedir?Yamuk, iki paralel kenarı ve iki farklı uzunlukta kenarı olan dörtgen bir geometrik şekildir. Matematikte, yamukların alanını hesaplamak için özel bir formül bulunmaktadır. Bu formül, yamukların özelliklerine bağlı olarak alanın ne şekilde hesaplanacağına dair önemli bilgiler sunar. Yamuk alanının hesaplanmasında kullanılan formül, aşağıdaki gibidir: Yamuk Alan Formülü Yamuk alanını hesaplamak için kullanılan formül şu şekildedir: A = (a + b) / 2 hBurada;- A: Yamuk alanı- a: Üst kenar uzunluğu- b: Alt kenar uzunluğu- h: Yamuk yüksekliğiBu formül, yamukların alanını hesaplamak için en yaygın kullanılan yöntemdir. Üst ve alt kenar uzunlukları ile yükseklik değerinin bilinmesi, yamuk alanını kolaylıkla bulmamıza olanak tanır. Yamuk Türleri Yamuklar, çeşitli türlere ayrılabilir. Bu türler, yamukların kenar uzunlukları ve açılarına göre farklılık gösterir. Temel olarak iki ana tür bulunmaktadır:
Her iki türün de alan hesaplama yöntemi aynıdır, ancak kenar uzunlukları ve yükseklikleri farklılık gösterebilir. İkizkenar Yamuk İkizkenar yamuk, iki kenarı eşit uzunlukta olan ve paralel kenarları bulunan bir yamuk türüdür. Bu yamuk, simetrik özelliklere sahiptir ve genellikle daha estetik bir görünüme sahiptir. Çeşitkenar Yamuk Çeşitkenar yamuk, kenar uzunluklarının birbirinden farklı olduğu bir yamuk türüdür. Bu tür yamuklar, daha düzensiz bir görünüme sahiptir ve alan hesaplaması açısından daha karmaşık olabilir. Ancak yukarıda belirtilen formül her iki tür için de geçerlidir. Yamuk Alanının Uygulamaları Yamuk alan formülü, birçok alanda uygulama bulmaktadır. Bu uygulamalardan bazıları şunlardır:
Yamukların alanlarının doğru bir şekilde hesaplanması, bu alanlarda etkin bir şekilde çalışabilmek için gereklidir. Ekstra Bilgiler Yamukların alan hesaplaması dışında, çevre hesaplaması da yapılabilmektedir. Yamuk çevresi, tüm kenar uzunluklarının toplamına eşittir. Çevreyi hesaplamak için aşağıdaki formül kullanılabilir: C = a + b + c + dBurada;- C: Yamuk çevresi- c ve d: Yamukta yer alan diğer iki kenar uzunluğuBu hesaplama, yamukların fiziksel özelliklerini anlamak ve çeşitli uygulamalarda kullanılmak üzere önemlidir. Sonuç olarak, yamuk alan formülü, geometrik şekillerin temel taşlarından biri olup, çeşitli alanlarda uygulama bulmaktadır. Yamukların özelliklerini ve alan hesaplama yöntemlerini bilmek, matematiksel becerilerin geliştirilmesine katkı sağlar. Bu bilgi, öğrenciler ve profesyoneller için önemlidir. |
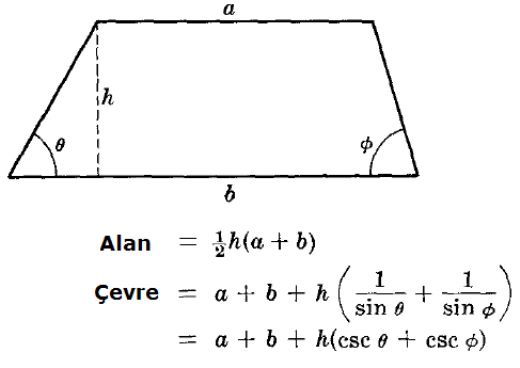















































Yamukların alanını bulmak için doğru bir yöntem izlemek önemli. Dik yamuğun alanı nasıl bulunur sorusu çokça merak ediliyor. Yamuğun taban uzunlukları ve yüksekliği ile hesaplanırken, formül A = ((a + b) / 2) h kullanılıyor. Bu formülü bilmek, alan hesaplamalarını kolaylaştırıyor.
Dik Yamukların Alanı
Derda, dik yamukların alanını bulmak için doğru bir yaklaşım sergilediğinizi belirtmek isterim. Dediğin gibi, dik yamukların alanını hesaplamak için kullanılan formül oldukça basit ve etkili.
Formülün Kullanımı
A = ((a + b) / 2) h formülü, yukarıda belirttiğin gibi, yamukların taban uzunlukları (a ve b) ile yükseklik (h) değerlerini kullanarak alanı hesaplamamıza olanak tanıyor. Bu formül, alan hesaplamalarını kolaylaştırdığı gibi, aynı zamanda geometri ile ilgili temel bilgileri pekiştirmemize de yardımcı oluyor.
Uygulama
Bu formülü kullanarak pratik yapman, konuyu daha iyi anlamanı sağlayacaktır. Farklı değerlerle hesaplamalar yapmak, dik yamukların alanını bulma becerini geliştirecektir. Geometri derslerinde bu tür uygulamalar oldukça faydalıdır. Başarılarının devamını dilerim!
Yamuk alan hesaplama, matematiksel kavramlar arasında oldukça önemli bir yer tutuyor. Özellikle ikizkenar yamuklarda tabanların eşitliği ve yükseklik bilgisiyle alanın hesaplanması, geometri derslerinde sıkça karşılaşılan bir durum. Yamuk alan formülünü bilmek, bu tür soruları kolayca çözebilmemizi sağlıyor.
Yamuk Alan Hesaplamanın Önemi
Kadın, yamuk alan hesaplama, matematikte temel bir kavram olarak karşımıza çıkıyor ve birçok alanda uygulama alanı buluyor. Özellikle ikizkenar yamuklar gibi özel durumlar, geometri derslerinde sıkça ele alınıyor. Bu tür soruları çözebilmek, matematiksel düşünme becerimizi geliştirirken, aynı zamanda pratikte de fayda sağlıyor.
İkizkenar Yamuklarda Alan Hesaplama
İkizkenar yamuklar, tabanlarının eşit olduğu durumlar nedeniyle alan hesaplaması açısından oldukça elverişli. Yükseklik bilgisi ile birlikte taban uzunluklarını bildiğimizde, alanı hesaplamak için kullanacağımız formül, matematiksel işlemleri kolaylaştırıyor. Bu nedenle, bu formülü iyi bilmek ve uygulamak, geometri derslerindeki başarıyı artırıyor.
Sonuç
Sonuç olarak, yamuk alan hesaplama, sadece matematiksel bir bilgi olarak kalmayıp, günlük yaşamda karşılaşabileceğimiz birçok durumu anlamamızda da yardımcı oluyor. Bu nedenle, bu konudaki bilginizi geliştirmek, hem akademik başarı hem de pratikteki uygulamalar için oldukça faydalı olacaktır.
Yamuk alanı hakkında bilgileri okuduktan sonra, yamukların özelliklerini düşünmek oldukça ilginç. Özellikle ikizkenar yamukların simetrik yapısı ve taban açıları arasındaki eşitlik dikkat çekiyor. Sizce bu yamuk alan özellikleri, mimaride nasıl bir etki yaratır?
Tayuk, yamuk alanının mimarideki etkileri gerçekten oldukça ilginçtir. Özellikle ikizkenar yamukların simetrik yapısı, mimari tasarımlara estetik bir denge katabilir. Bu yapılar, görsel olarak hoş bir görünüm sunarak, mekanların daha çekici hale gelmesini sağlar.
Fonksiyonel Kullanım: İkizkenar yamuklar, yapısal olarak da avantajlar sunar. Bu tür şekiller, yük dağılımını daha etkili bir şekilde sağlayabilir, böylece binaların dayanıklılığı artar. Ayrıca, alanın daha verimli kullanılması için de uygun bir zemin oluşturabilirler.
Estetik ve Simetri: Mimaride simetri, göz alıcı bir estetik yaratır. İkizkenar yamuklar, mimari tasarımlara simetrik bir yapı ekleyerek, izleyicinin dikkatini çekebilir. Bu, özellikle giriş alanları veya önemli yapısal unsurlar için etkileyici bir tasarım unsuru olabilir.
Sonuç: Kısacası, ikizkenar yamukların mimarideki kullanımı, hem estetik hem de işlevsel açıdan önemli avantajlar sağlar. Bu özellikler, tasarımların hem görsel çekiciliğini artırırken hem de yapısal sağlamlık sunar. Mimaride bu tür geometrik şekillerin kullanılması, yaratıcı ve yenilikçi tasarımlar için ilham kaynağı olabilir.
Ya, yamuğun alanını hesaplarken neden paralel kenarlarla yüksekliği kullanıyoruz? Yanal kenarların uzunluğu bu hesaplamada neden önemli değil?
Naile,
Paralel Kenar ve Yükseklik: Yamuğun alanını hesaplarken kullanılan formül, yamuk tabanlarının uzunlukları ile bu tabanlar arasındaki dik mesafeyi, yani yüksekliği kullanır. Bu yöntem, yamuk içindeki tüm alanı doğrudan hesaplamak için tasarlanmıştır.
Yanal Kenarlar: Yanal kenarlar, yamuk alanını hesaplarken doğrudan bir rol oynamaz. Bu kenarların uzunlukları, yamuğun şekli ve yapısı hakkında bilgi verse de, alanın kendisini belirlemezler. Alan hesaplamasında önemli olan, tabanlar ve yükseklik arasındaki dik mesafedir.
Umarım bu açıklama yardımcı olur!