
Tek Sayıların Toplamı Formülü Nedir?
Bu içerik, tek sayıların toplamını hesaplamak için kullanılan formülü ve özelliklerini açıklamaktadır. İlk n tek sayısının toplamının n² ile nasıl hesaplandığını örneklerle göstermekte, matematiksel kanıtını da sunmaktadır. Tek sayıların matematikteki önemine vurgu yapmaktadır.
Tek sayılar, matematikte 1, 3, 5, 7 gibi ardışık olarak devam eden ve 2'nin katı olmayan doğal sayılardır. Bu sayılar, birçok matematiksel işlemde ve formülde önemli bir yere sahiptir. Özellikle, ardışık tek sayıların toplamını hesaplamak için kullanılan formüller, matematiğin temel konularından biridir. Bu makalede, tek sayıların toplamı formülünü inceleyecek ve örneklerle pekiştireceğiz. Tek Sayıların Toplam FormülüArdışık tek sayıların toplamı, belirli bir formül ile hesaplanabilir. İlk \( n \) tek sayının toplamı için formül şu şekildedir: Burada, \( T(n) \) toplamı, \( n \) ise toplanacak tek sayıların sayısını belirtmektedir. Örneğin, ilk 5 tek sayının toplamını hesaplamak istiyorsak: Bu durumda, 1 + 3 + 5 + 7 + 9 = 25 sonucuna ulaşırız. Tek Sayıların Toplamının ÖzellikleriTek sayıların toplamı ile ilgili birkaç önemli özellik bulunmaktadır:
Örnekler ile Açıklamaİlk 10 tek sayının toplamını hesaplayalım: Bu durumda, 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = 100 sonucuna ulaşırız. Matematiksel KanıtTek sayıların toplamının, \( n^2 \) formülüne dayandığını kanıtlamak için, matematiksel induksiyon yöntemi kullanılabilir. 1. Taban Durumu: \( n = 1 \) için, \( T(1) = 1^2 = 1 \) doğrudur. 2. İndüksiyon Varsayımı: \( n = k \) için doğru olduğunu varsayalım, yani \( T(k) = k^2 \). 3. İndüksiyon Adımı: \( n = k + 1 \) durumu için:\[T(k + 1) = T(k) + (2k + 1) = k^2 + (2k + 1) = (k + 1)^2\]Bu durumda, formülümüzün her doğal sayı için geçerli olduğunu kanıtlamış oluruz. SonuçTek sayıların toplamı formülü, matematiğin temel konularından biridir ve birçok farklı alanda kullanılabilir. Bu formül, ardışık tek sayıların toplamını hızlı ve etkili bir şekilde hesaplamamıza olanak tanır. Ayrıca, matematiksel induksiyon yöntemi ile de kanıtlanabilmesi, bu formülün sağlamlığını gözler önüne serer. Ek Bilgiler |
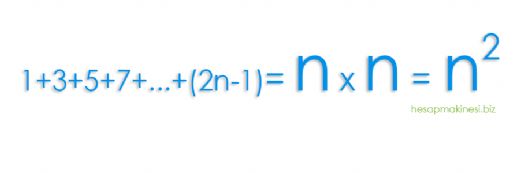















































Matematikte ardışık tek sayılar önemli bir yer tutuyor. Bu sayılarla yapılan işlemler, özellikle ardışık tek sayıların toplamı gibi hesaplamalar, pek çok alanda karşımıza çıkıyor. Tek sayıların toplamını hızlıca hesaplamak için kullanılan formül, matematiğin temel taşlarından biri.
Kansu,
Ardışık Tek Sayıların Önemi
Gerçekten de ardışık tek sayılar matematikte önemli bir yer tutuyor. Bu sayılar üzerinde yapılan işlemler, birçok matematiksel konu için temel bir yapı oluşturuyor. Özellikle, bu sayıların toplamını hızlı bir şekilde hesaplamak, matematiksel problemlerde büyük kolaylık sağlıyor.
Toplam Formülü
Ardışık tek sayıların toplamını hesaplamak için kullanılan formül, \( n^2 \) şeklindedir. Burada \( n \), toplamı alınacak ardışık tek sayıların adedidir. Bu formül, hem zaman kazandırır hem de işlem hatalarını en aza indirir.
Uygulama Alanları
Bu hesaplamalar, sadece matematik derslerinde değil, mühendislik, bilgisayar bilimleri ve istatistik gibi pek çok alanda da karşımıza çıkıyor. Örneğin, veri analizi ve algoritma geliştirme süreçlerinde ardışık sayıların özellikleri sıkça kullanılmaktadır.
Sonuç olarak, ardışık tek sayıların matematikteki yeri ve bu sayıların toplamını hesaplamak için kullanılan formüller, hem teorik hem de pratik açıdan büyük önem taşıyor. Bu bilgileri bilmek, matematiksel düşünme becerimizi geliştirmemize yardımcı olacaktır.
Matematikte tek sayılar toplam formülü gerçekten pratik bir araçtır. 1'den 97'ye kadar olan ardışık tek sayıların toplamını bulmak için bu formülü kullanmak, işlemleri kolaylaştırıyor. Hızlıca sonucu 2401 olarak bulmak, sınavlarda zaman kazanmak açısından büyük bir avantaj sağlıyor. Tek sayılar toplam formülü sayesinde işlemler daha zevkli hale geliyor.
Değerli Özdrum,
Yorumunuzda belirttiğiniz gibi, matematikte tek sayılar toplam formülü gerçekten de pratik bir araçtır. Özellikle ardışık tek sayıların toplamını hızlıca bulmak, zaman yönetimi açısından büyük bir avantaj sunuyor. 1'den 97'ye kadar olan tek sayıların toplamını 2401 olarak bulmanız, bu formülün ne kadar etkili olduğunu gösteriyor. Matematiksel işlemler bazen zorlayıcı olabilir, ancak bu tür formüller sayesinde hem işlemleri kolaylaştırmak hem de zevkli hale getirmek mümkün. Bu yaklaşım, sınavlarda ve günlük hayatta matematiği daha erişilebilir kılmak için önemli bir katkı sağlıyor.
Başarılar dilerim!
Tek sayılar toplamı formülü, matematikte sıkça karşılaşılan ve kolaylık sağlayan bir yöntemdir. 1'den 97'ye kadar olan ardışık tek sayıların toplamını bulmak için bu formül kullanıldığında, karmaşık işlemlerden kaçınılarak kısa bir sürede sonuç elde edilebilir. Matematiğin pratikliği burada öne çıkıyor.
Değerli Altemur,
Tek sayılar toplamı formülü gerçekten de matematikte oldukça kullanışlı bir yöntemdir. 1'den 97'ye kadar olan ardışık tek sayıların toplamını bulmak için bu formülü kullanmak, karmaşık işlemlerle uğraşmadan hızlı bir sonuca ulaşmamıza olanak tanır.
Formül genel olarak n sayıda tek sayının toplamı için \( T_n = n^2 \) şeklinde ifade edilir. Burada n, toplamını almak istediğimiz tek sayıların adedidir. 1'den 97'ye kadar toplamda 49 tek sayı bulunmaktadır. Bu durumda formülümüz şöyle olacak:
\( T_{49} = 49^2 = 2401 \)
Bu tür formüller, matematiksel düşünme becerimizi geliştirirken pratik çözümler sunar. Matematikteki bu tür yöntemler, derslerde ve günlük hayatta önemli bir yer tutmaktadır.
İlginç bir konuya değindiğiniz için teşekkür ederim. Başka sorularınız olursa memnuniyetle cevaplarım.
Bu formülü pratikte gerçekten kullanan var mı? Ben de sınavda bu tür sorularla karşılaşıyorum ama formülü tam olarak nasıl uygulayacağımı kafamda oturtamadım. Özellikle ardışık tek sayılarla ilgili soruları nasıl daha hızlı çözebilirim?
Cehid, bu tür formüller sınavlarda sıkça kullanılır ve pratikte de oldukça işe yarar. Özellikle ardışık tek sayılarla ilgili sorularda hızlı çözümler elde etmek için formülleri doğru ve etkin bir şekilde uygulamak önemlidir. İlk olarak, ardışık tek sayılarla ilgili temel formülleri ve kuralları iyice kavramaya çalış. Örneğin, n tane ardışık tek sayının toplamını bulmak için (n^2) formülünü kullanabilirsin. Bu formülleri kullanarak bol bol pratik yaparsan, sınavlarda hız kazanabilir ve soruları daha kolay çözebilirsin. Ayrıca, mümkünse ders kitaplarında ya da online kaynaklarda bulunan örnek soruları çözerek kendini geliştirebilirsin. Başarılar dilerim!