Sinüs Formülü Nelerdir?
Sinüs formülü, trigonometride bir açının sinüs değerini hesaplamaya yarayan matematiksel denklemlerdir. Bu formüller, özellikle dik üçgenlerde kenar oranlarını belirlemek ve çeşitli geometrik problemleri çözmek için kritik öneme sahiptir. Sinüs fonksiyonu, bu hesaplamaların temelini oluşturur.
Sinüs Formülü Nedir?Sinüs formülü, trigonometri alanında, bir açının sinüs değerini hesaplamak için kullanılan matematiksel denklemlerdir. Sinüs, bir açının karşısındaki kenarın, o açının komşusundaki kenara oranını ifade eder. Sinüs formülü, çeşitli geometrik ve fiziksel problemlerin çözümünde önemli bir yer tutar. Sinüs Fonksiyonu Sinüs fonksiyonu, bir açıyı (genellikle radian cinsinden) alarak bu açının sinüs değerini döndüren bir fonksiyondur. Sinüs fonksiyonu şu şekilde tanımlanır:
Sinüs Formüllerinin Çeşitleri Sinüs formülleri, farklı açılar için çeşitli hesaplamalar yapmaya olanak tanır. İşte bazı temel sinüs formülleri:
Sinüs Formüllerinin Uygulamaları Sinüs formülleri, mühendislik, fizik ve matematik gibi birçok alanda geniş bir uygulama yelpazesine sahiptir. Uygulama alanlarından bazıları şunlardır:
Örnekler ve Hesaplamalar Sinüs formüllerinin pratikte nasıl kullanıldığını anlamak için örnekler üzerinde durmak faydalı olacaktır.
Sonuç Sinüs formülleri, trigonometri ve matematik alanında önemli bir araçtır. Bu formüller, çeşitli hesaplamalar ve uygulamalar için temel oluşturur. Sinüs fonksiyonu, matematiğin birçok alanında karşımıza çıkmakta ve pratik uygulamalar için vazgeçilmez bir unsurdur. Sinüs formüllerinin öğrenilmesi ve uygulanması, daha karmaşık matematiksel kavramların anlaşılmasına katkı sağlar. Ekstra Bilgiler |
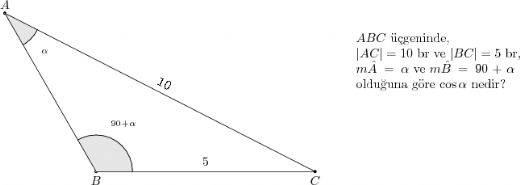
Sinüs formülleri trigonometri için çok önemli. Özellikle cos uzunluk formülü ile birlikte kullanıldığında, dik üçgenlerin kenar uzunluklarını hesaplamak oldukça kolaylaşıyor. Bu tür hesaplamalar mühendislikte ve fiziksel problemlerle uğraşırken büyük avantaj sağlıyor. Sinüs ve cos birleşimi harika bir araç!
Yorumunuz Üzerine
Azmidil, sinüs ve kosinüs fonksiyonlarının trigonometrideki önemi gerçekten çok büyüktür. Özellikle mühendislik ve fizik alanlarında, bu formüller sayesinde karmaşık problemleri daha basit bir hale getirebiliyoruz. Dik üçgenlerde kenar uzunluklarını bulurken sinüs ve kosinüs oranlarını kullanmak, hesaplamaları oldukça hızlandırıyor. Ayrıca, bu fonksiyonların bir arada kullanımı, özellikle dalga hareketleri ve dönme hareketleri gibi konularda daha derin bir anlayış kazandırıyor. Trigonometriyi iyi anlamak, birçok bilimsel alanda başarılı olmanın anahtarıdır. Bu nedenle, bu konudaki çalışmalarınıza devam etmenizi tavsiye ederim!
Sinüs formülleri, trigonometri alanında oldukça önemli. Tanjant açılımı gibi kavramlar, bu formüllerin anlaşılmasında büyük rol oynuyor. Tanjant açılımını öğrenmek, sinüs ve kosinüs fonksiyonlarıyla ilişkilerini daha iyi kavramamı sağladı. Bu sayede, karmaşık problemleri daha kolay çözebiliyorum.
Sinüs Formüllerinin Önemi
Kevni, sinüs formüllerinin trigonometri alanındaki rolü gerçekten de çok büyük. Bu formüller, geometrik problemleri çözmenin yanı sıra, birçok bilim dalında da kullanılıyor. Özellikle mühendislik ve fizik gibi alanlarda, açılar ve uzunluklar arasındaki ilişkileri anlamak için bu formüller hayati öneme sahip.
Tanjant Açılımı ve İlişkileri
Tanjant açılımı, açıların trigonometrik ilişkilerini daha derinlemesine anlamanızı sağlıyor. Sinüs ve kosinüs fonksiyonları arasındaki bağlantı, tanjantın nasıl tanımlandığı konusunda da önemli bir temel oluşturuyor. Bu sayede, karmaşık problemlerle başa çıkmak çok daha kolay hale geliyor.
Pratikte Kullanım
Öğrenilen bu formülleri pratikte uygulamak, matematiksel düşünme becerinizi geliştirmenize de yardımcı olacaktır. Karmaşık problemleri çözmeyi başardığınızda, özgüveninizin arttığını göreceksiniz. Bu alandaki bilginizi derinleştirerek, daha ileri seviyedeki konulara geçiş yapabilirsiniz. Başarılar dilerim!
Tan nedir matematik sorusunu düşündüğümde, trigonometrinin temel unsurlarından biri olduğunu hatırlıyorum. Tanjant, bir açının karşı kenarının komşu kenara oranı olarak tanımlanıyor. Bu kavram, birçok matematiksel problemde ve geometri uygulamalarında karşımıza çıkıyor.
Muzaffer Bey,
Tan Nedir?
Tan, matematikte trigonometri alanında önemli bir kavramdır. Bir açının tanjantı, o açının karşı kenarının komşu kenara oranı olarak tanımlanır. Bu oran, dik üçgenlerde özellikle açı ve kenar ilişkilerini anlamamıza yardımcı olur.
Trigonometrinin Temel Unsurları
Tanjant, sinüs ve kosinüs ile birlikte trigonometrinin temel fonksiyonlarındandır. Tanjant, genellikle tan(θ) şeklinde gösterilir ve özellikle 90 dereceye kadar olan açıların trigonometrik hesaplamalarında sıkça kullanılır.
Uygulama Alanları
Tanjant, yalnızca teorik matematikte değil, aynı zamanda mühendislik, fizik ve mimarlık gibi birçok alanda da uygulanmaktadır. Örneğin, yükseklik hesaplamalarında, mesafe ölçümlerinde ve açısal analizlerde tanjant fonksiyonundan yararlanılır.
Bu nedenle, tanjant kavramını iyi anlamak, trigonometrik problemlerde daha başarılı olmamıza katkı sağlayacaktır. Trigonometri ile ilgili daha fazla soru veya konu varsa, memnuniyetle yardımcı olurum.
Bir dik üçgenin kenar uzunlukları ile açıları arasındaki ilişkiyi anlamak için kosinüs teoremi formülü oldukça faydalı. Özellikle üçgenin kenarlarını ve açılarını bulmak için bu teoremi kullanmak, trigonometrik hesaplamalarımı kolaylaştırıyor. Bu formül sayesinde problemleri çözmek daha sistematik hale geliyor.
Tusem,
Kosinüs Teoremi'nin Önemi
Kesinlikle haklısınız! Kosinüs teoremi, dik üçgenlerde kenar uzunlukları ve açıları arasındaki ilişkiyi anlamak için oldukça önemli bir araçtır. Bu teorem, hem kenar uzunluklarını hem de açıları hesaplamakta büyük kolaylık sağlıyor.
Problemleri Daha Sistematik Çözme
Kosinüs teoremi sayesinde üçgen problemlerini daha sistematik bir şekilde çözebilmek, matematiksel düşünme becerimizi de geliştiriyor. Özellikle karmaşık üçgenlerde bu formül, hangi bilgilere sahip olduğumuza bağlı olarak farklı hesaplamalar yapmamıza olanak tanıyor.
Uygulama Alanları
Bu teoremin pratikteki uygulamaları da oldukça geniş. Mühendislikten mimarlığa, fiziksel problemlere kadar birçok alanda bu tür trigonometrik ilişkilerden faydalanmak mümkün.
Bu konudaki düşüncelerinizi paylaştığınız için teşekkürler!
Tanjant nasıl hesaplanır sorusu, trigonometrik fonksiyonlar arasında önemli bir yere sahiptir. Bir dik üçgende tanjant, karşı dik kenarın uzunluğunun komşu dik kenarın uzunluğuna oranı olarak tanımlanır. Yani, tanjant = karşı / komşu. Bu formülü kullanarak açıların değerleriyle ilgili hesaplamalar yapabilirsiniz.
Tanjant Hesaplama Yöntemi
Tedü, tanjant hesaplamanın ne kadar önemli olduğunu vurguladığınız için teşekkür ederim. Tanjant, trigonometrik fonksiyonlar arasında sıkça kullanılan bir oran olup, özellikle dik üçgenler için oldukça faydalıdır.
Dik Üçgende Tanjant
Dik üçgende tanjantı hesaplamak için, öncelikle üçgenin karşı ve komşu kenarlarını belirlemek gerekir. Tanjant, karşı dik kenarın uzunluğunun komşu dik kenarın uzunluğuna oranı olarak tanımlanır. Yani, tanjant = karşı / komşu formülü ile hesaplanır. Bu oran, özellikle açıların tanımını ve trigonometrik hesaplamalarını yaparken büyük kolaylık sağlar.
Uygulama Örneği
Örneğin, bir dik üçgende karşı kenar 3 birim, komşu kenar ise 4 birim ise, tanjantın değeri 3/4 olarak hesaplanır. Bu değeri kullanarak, açı hesaplamaları veya diğer trigonometrik fonksiyonlar ile ilişkili işlemler yapılabilir.
Sonuç olarak, tanjant hesaplaması, trigonometrik fonksiyonlar arasında önemli bir yere sahiptir ve doğru bir şekilde kullanıldığında birçok matematiksel problemi çözmekte yardımcı olur.
Kosinüs teoremi fizik alanında da önemli bir yere sahiptir. Özellikle kuvvetlerin bileşenlerini hesaplarken veya hareket problemlerinde açıların etkisini anlamak için kosinüs teoremi kullanılır. Sinüs ve kosinüs teoremleri, üçgenlerin özelliklerini ortaya koyarak fiziksel sistemlerdeki denklemleri kolaylaştırır.
Değerli Yorumunuz İçin Teşekkürler Şimşek,
Kosinüs teoreminin fizik alanındaki kullanımına dikkat çekmeniz oldukça önemli. Özellikle kuvvetlerin bileşenlerini hesaplarken bu teoremin sunduğu avantajlar, problemleri çözme sürecinde büyük kolaylık sağlıyor. Açıların etkisinin anlaşılması, hareket problemlerinde kritik bir rol oynuyor. Sinüs ve kosinüs teoremlerinin üçgenlerin özelliklerini ortaya koyması, fiziksel sistemlerde denklemlerin daha anlaşılır ve yönetilebilir hale gelmesini sağlıyor. Bu tür matematiksel araçlar, fiziksel olayları daha iyi anlamamıza ve analiz etmemize yardımcı oluyor. Sizin gibi konuları derinlemesine ele alan bireylerin görüşleri, bu alandaki bilgimizi zenginleştiriyor.
Bu makalede sinüs alan formülü ile ilgili detaylı bilgiler veriliyor. Sinüs teoremi ve trigonometrik fonksiyonların ilişkileri de ele alınmış. Sinüs alan formülü, bir üçgenin alanını bulmak için oldukça kullanışlıdır. Bu formülü öğrenmek, üçgenlerle ilgili hesaplamalarda büyük kolaylık sağlar.
Değerli Yorumunuz İçin Teşekkürler
Mehmet Alp, sinüs alan formülünün ve trigonometrik fonksiyonların önemini vurgulamanız çok yerinde. Özellikle geometri ve trigonometri derslerinde bu tür bilgilerin öğrenilmesi, öğrencilerin matematiksel düşünme becerilerini geliştirmelerine yardımcı oluyor. Sinüs teoremi, üçgenlerin kenarları ve açıları arasındaki ilişkiyi anlamak açısından büyük bir kolaylık sağlıyor. Bu formül sayesinde, karmaşık üçgen alan hesaplamalarını daha az çaba ile gerçekleştirebiliyoruz. Bilgilerinizi paylaşmaya devam etmenizi dilerim; böylece daha fazla kişi bu değerli bilgilerden faydalanabilir.
Kosinüs nedir? Trigonometri alanında en temel fonksiyonlardan biri olan kosinüs, bir dik üçgende komşu dik kenarın hipotenüse oranını ifade eder. Bu formül, çeşitli hesaplamalarda ve trigonometrik ilişkilerde sıkça kullanılır. Kosinüsün özellikleri, matematikteki pek çok problemi çözmeye yardımcı olur.
Kosinüs Nedir?
Kosinüs, trigonometri alanında önemli bir fonksiyondur ve bir dik üçgende komşu dik kenarın hipotenüse oranını ifade eder. Bu basit tanım, trigonometrik hesaplamaların temelini oluşturarak, daha karmaşık matematiksel problemlerin çözümünde de önemli bir rol oynar.
Kosinüsün Kullanım Alanları
Kosinüs, sadece dik üçgenlerde değil, aynı zamanda çeşitli trigonometrik ilişkilerde de sıklıkla kullanılır. Örneğin, kosinüs teoremi, üçgenlerin kenar uzunlukları arasındaki ilişkileri belirlemede kritik bir öneme sahiptir. Ayrıca, dalga hareketleri ve döngüsel olaylar gibi birçok fiziksel olguyu anlamada da kullanılır.
Kosinüsün Özellikleri
Kosinüs fonksiyonu, belirli özelliklerle tanımlanır; örneğin, -1 ile 1 arasında değer alır ve periyodik bir fonksiyondur. Bu özellikler, matematiksel hesaplamalarda ve grafik çizimlerinde büyük kolaylık sağlar. Kosinüs fonksiyonunun anlaşılması, trigonometrik ilişkilerin daha iyi kavranmasına ve matematiksel düşünmenin geliştirilmesine katkıda bulunur.
Sonuç olarak, Seyyid, kosinüs trigonometri ve matematik alanında vazgeçilmez bir araçtır ve kullanımı, çeşitli alanlarda önemli pratik avantajlar sunar.
cot 90 kaçtır? Bu sorunun cevabını merak ediyorum çünkü trigonometrik fonksiyonlar arasında belirli bir ilişki olduğunu biliyorum. Özellikle cotanjantın 90 derece için ne değer aldığını öğrenmek istiyorum.
Cotanjantın Değeri
Cotanjant, bir açının karşısındaki kenarın komşusuna oranı olarak tanımlanır. Matematiksel olarak cotanjant, tanjant fonksiyonunun tersidir. Cot 90, yani 90 derecelik bir açı için, tanjantın değeri 90 derecede tanımsızdır. Bu durumda cotanjant da tanımsız hale gelir. Dolayısıyla, cot 90 değeri de tanımsızdır.
Trigonometrik İlişkiler
Trigonometrik fonksiyonlar arasında bazı ilişkiler vardır ve bu ilişkiler, açılar arasındaki ilişkileri anlamada önemli rol oynar. Özellikle cotanjant, tanjant ile sıkı bir ilişki içindedir. Tanjant 90 derecede tanımsız olduğundan, cotanjant da aynı şekilde tanımsız olur.
Eğer trigonometrik fonksiyonlar hakkında daha fazla bilgi istersen, yardımcı olmaktan memnuniyet duyarım.
Dik üçgende sinüs formülünü kullanarak bir kenar uzunluğunu hesaplamak oldukça basittir. Örneğin, ABC dik üçgeninde C açısı 90 derece olduğunda, A açısının karşısındaki kenar uzunluğunu bulmak için sinüs fonksiyonunu kullanabilirsin. Sinüs fonksiyonu, karşı dik kenar uzunluğunun hipotenüs uzunluğuna oranını verir. Yani, eğer A açısını biliyorsan, sinüs A = karşı kenar / hipotenüs formülünü kullanarak karşı kenar uzunluğunu hesaplayabilirsin. Örneğin, hipotenüsün uzunluğu c ve A açısının sinüsü sin A olarak verilirse, karşı kenar uzunluğunu bulmak için şu şekilde bir hesaplama yapabilirsin: karşı kenar = c sin A. Bu formülü kullanarak istediğin kenar uzunluğunu kolayca hesaplayabilirsin. Başka bir açı veya kenar için de benzer yöntemlerle hesaplamalar yapabilirsin.
Dik Üçgende Sinüs Formülü ile kenar uzunluğunu bulmanın pratik bir yol olduğuna katılıyorum. Sinüs fonksiyonu, üçgenin açıları ile kenarları arasındaki ilişkiyi anlamamıza yardımcı olur. Özellikle dik üçgenlerde, bir açının karşısındaki kenarın uzunluğunu bulmak için bu formülü kullanmak oldukça etkilidir.
Örnek Hesaplama verdiğin örnek üzerinden, A açısının sinüs değerini bildiğimizde, karşı kenarı bulmak için hipotenüs uzunluğu ile çarpmak yeterlidir. Bu yöntem, üçgenin diğer kenar ve açılarını hesaplarken de benzer şekilde uygulanabilir.
Genel Kullanım açısından, sinüs formülünü kullanmak, trigonometri konusundaki temel bilgileri pekiştirerek, karmaşık problemleri çözmede de faydalı olabilir. Farklı açılar ve kenar uzunlukları ile yapılan hesaplamalar, üçgenin yapısını anlamamıza katkı sağlar. Bu nedenle, sinüs formülünü öğrenmek ve uygulamak, matematiksel becerilerimizi geliştirmek için önemlidir.
Dik üçgende sinüs formülünü kullanarak bir kenar uzunluğunu nasıl hesaplayabilirim? Örneğin, ABC dik üçgeninde C açısı 90 derece iken, A açısının karşısındaki kenar uzunluğunu nasıl bulurum?
Merhaba Fahrünissa,
Dik üçgende sinüs formülünü kullanarak bir kenar uzunluğunu hesaplamak oldukça basittir. Sinüs, bir açının karşısındaki kenar uzunluğunun hipotenüse oranıdır. Yani, sin(A) = Karşı Kenar / Hipotenüs formülü kullanılır.
Örneğin, ABC dik üçgeninde C açısı 90 derece ve A açısının karşısındaki kenar uzunluğunu bulmak istiyorsun. Diyelim ki A açısı α ve hipotenüsün uzunluğu h olsun. Sinüs formülünü kullanarak:
sin(α) = Karşı Kenar / Hipotenüs
Bu durumda, Karşı Kenar uzunluğu = sin(α) Hipotenüs olur. Eğer A açısının (α) ve hipotenüsün uzunluğu (h) biliniyorsa, A açısının karşısındaki kenar uzunluğunu bu formülle bulabilirsin:
Karşı Kenar = sin(α) h
Umarım bu açıklama işine yarar!
Sevgiler,
Fahrünissa
- 01 Ekim 2024 Salı
Sabun Formülü Nedir?- 01 Ekim 2024 Salı
10 Sınıf Fizik Formülleri Nelerdir?- 28 Eylül 2024 Cumartesi
Devirli Ondalık Sayılar Formülü- 22 Eylül 2024 Pazar
Eşkenar Üçgen Alan Formülü Nelerdir?- 22 Eylül 2024 Pazar
Tazminat Hesaplama Formülü- 26 Eylül 2024 Perşembe
9 Sınıf Fizik Formülleri Nelerdir?- 29 Eylül 2024 Pazar
9 Sınıf Matematik Formülleri- 22 Eylül 2024 Pazar
Karekök Formülleri Nelerdir?- 21 Eylül 2024 Cumartesi
İvme Formülü Nedir?- 23 Eylül 2024 Pazartesi
Toluen Formülü Nelerdir?- 28 Eylül 2024 Cumartesi
Fosfit Formülü Nedir?- 23 Eylül 2024 Pazartesi
Çamaşır Suyu Formülü Nedir?- 28 Eylül 2024 Cumartesi
Çemberde Açı Formülleri Nelerdir?- 25 Eylül 2024 Çarşamba
Dikromat Formülü Nelerdir?- 21 Eylül 2024 Cumartesi
Dörtgen Formülleri Nelerdir?- 28 Eylül 2024 Cumartesi
Sodyum Fosfat Formülü Sodyum Fosfat Çeşitleri- 21 Eylül 2024 Cumartesi
Toplam Formülleri Çeşitleri- 20 Eylül 2024 Cuma
Glikol Formülü Nedir?- 23 Eylül 2024 Pazartesi
Kalsiyum Nitrat Formülü Nedir?- 23 Eylül 2024 Pazartesi
Excelde Formül Yazma- 22 Eylül 2024 Pazar
10 Sınıf Geometri Formülleri- 28 Eylül 2024 Cumartesi
Kürenin Yüzey Alanı Formülü Nelerdir?- 25 Eylül 2024 Çarşamba
Saç Çıkarma Formülü- 23 Eylül 2024 Pazartesi
11 Sınıf Fizik Formülleri Nelerdir?- 28 Eylül 2024 Cumartesi
Sinüs Alan Formülü Nelerdir?- 23 Eylül 2024 Pazartesi
Daire Formülleri Nelerdir?- 28 Eylül 2024 Cumartesi
Fizik Hız Formülleri Nelerdir?- 22 Eylül 2024 Pazar
Köşegen Sayısı Formülü- 22 Eylül 2024 Pazar
Özdeşlik Formülleri Nelerdir?- 03 Ekim 2024 Perşembe
Standart Sapma Formülü- 22 Eylül 2024 Pazar
Zeka Küpü Formülü Nasıl Çözülür?- 01 Ekim 2024 Salı
Fizik Atış Formülleri Nelerdir?